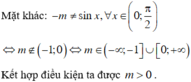Tìm m để hàm số y= (m-1)sinx+2 : sinx+m a) đồng biến trên khoảng (0;pi/2
RC
Những câu hỏi liên quan
Cho hàm số
y
(
m
-
1
)
sin
x
-
2
sin
x
-
m
. Tìm tất cả các giá trị của tham số m để hàm...
Đọc tiếp
Cho hàm số y = ( m - 1 ) sin x - 2 sin x - m . Tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng ( 0 ; π 2 ) .
A.
.
B.
.
C.
.
D.
.
Chọn A
Điều kiện: 
. Điều kiện cần để hàm số 
nghịch biến trên khoảng 
là
.
Ta có :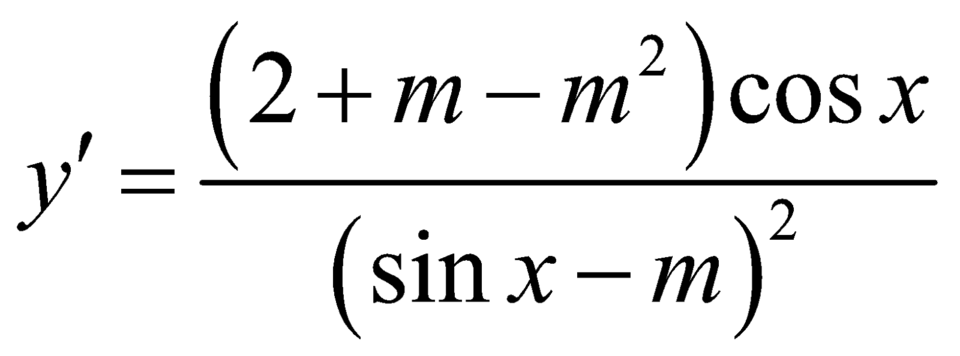 
.
Ta thấy 
.
Để ham số 
nghịch biến trên khoảng 
là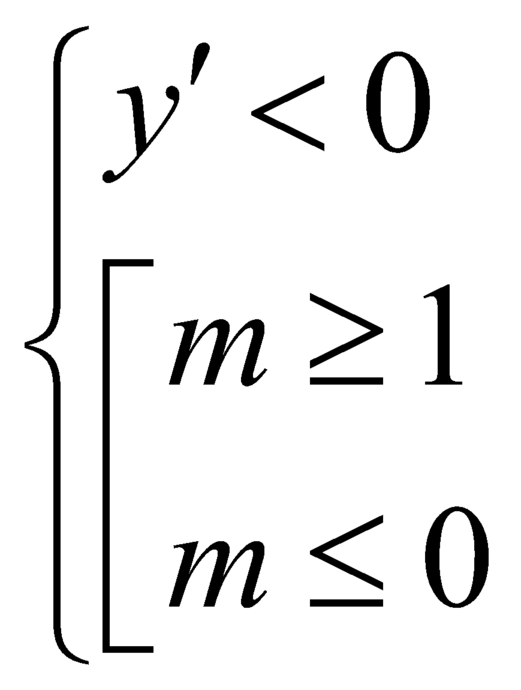
.
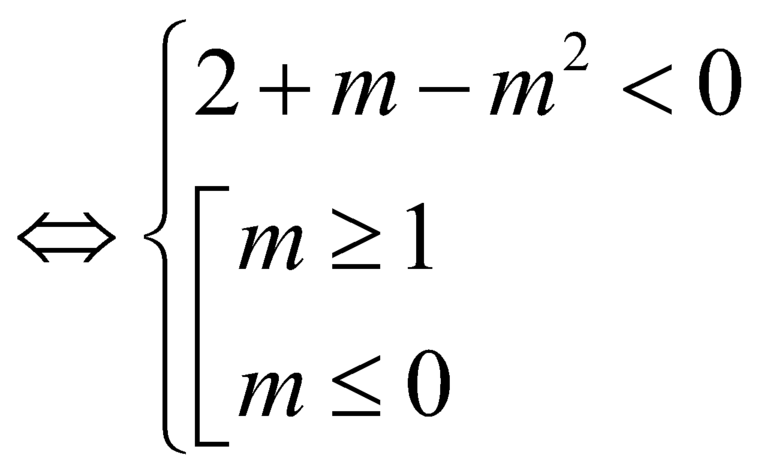
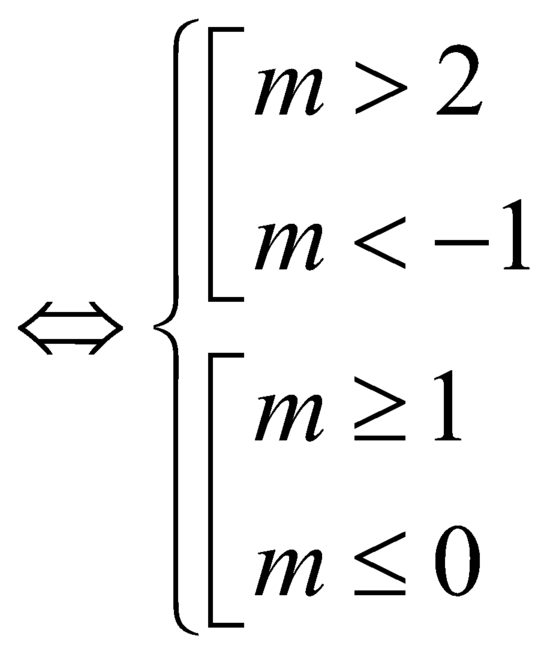
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
sinx
−
m
sinx
+
m
đồng biến trong khoảng
0
;
π
2
. A.
m
≥
0
B.
m
0
C. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = sinx − m sinx + m đồng biến trong khoảng 0 ; π 2 .
A. m ≥ 0
B. m > 0
C. − ∞ ; − 1 ∪ 0 ; + ∞
D. − ∞ ; − 1 ∪ 0 ; + ∞
Tìm tất cả các giá tri thưc của tham số m sao cho hàm số
y
s
inx
−
1
s
inx
−
m
đồng biến trên khoảng
0
;
π
2
. A. m 1 B.
m
≤
0
C. m 0 hoặc ...
Đọc tiếp
Tìm tất cả các giá tri thưc của tham số m sao cho hàm số y = s inx − 1 s inx − m đồng biến trên khoảng 0 ; π 2 .
A. m < 1
B. m ≤ 0
C. m < 0 hoặc m ≥ 1
D. 0 ≤ m ≤ 1
Đáp án B
Có y ' = − m + 1 cos x sin x − m 2 .
Vì x ∈ 0 ; π 2 ⇒ sin x ∈ 0 ; 1 .
Hàm số xác định trên 0 ; π 2 ⇔ m ∉ 0 ; 1 (1)
Hàm số đồng biến tên 0 ; π 2 ⇔ − m + 1 > 0 ⇔ m < 1 (2)
Kết hợp (1);(2) ta có m ≤ 0 .
Đúng 0
Bình luận (0)
Với giá trị nào của m thì hàm số
y
sin
x
-
m
sin
x
+
m
đồng biến trên khoảng
0
;
π
2
? A. m 0 B.
-
1
≤
m
0
C. -1 m 0 D. -1...
Đọc tiếp
Với giá trị nào của m thì hàm số y = sin x - m sin x + m đồng biến trên khoảng 0 ; π 2 ?
A. m > 0
B. - 1 ≤ m < 0
C. -1 < m < 0
D. -1 < m
Với giá trị nào của m thì hàm số
y
sinx
−
m
sinx
+
m
đồng biến trên khoảng
0
;
π
2
A.
-
1
m
B.
-
1
m
0...
Đọc tiếp
Với giá trị nào của m thì hàm số y = sinx − m sinx + m đồng biến trên khoảng 0 ; π 2
A. - 1 < m
B. - 1 < m < 0
C. m ≤ - 1
D. - 1 ≤ m ≤ 0
Với giá trị nào của m thì hàm số
y
sin
x
-
m
sin
x
+
m
đồng biến trên khoảng
0
;
π
2
? A. m 0 B. -1
≤
m 0 C. -1 m 0 D. -1 m
Đọc tiếp
Với giá trị nào của m thì hàm số y = sin x - m sin x + m đồng biến trên khoảng 0 ; π 2 ?
A. m > 0
B. -1 ≤ m < 0
C. -1 < m < 0
D. -1 < m
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số ysinx+cosx+mx đồng biến trên khoảng
-
∞
;
+
∞
A
.
-
2
≤
m
≤
2
B
.
m
≤
-
2
C
.
-
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=sinx+cosx+mx đồng biến trên khoảng - ∞ ; + ∞
A . - 2 ≤ m ≤ 2
B . m ≤ - 2
C . - 2 < m < 2
D . m ≥ 2
Tìm giá trị của m để hàm số y x + m(sinx + cosx + m ) luôn đồng biến trên R A.
-
2
2
≤
m
≤
2
2
B.
0
≤
m
≤
2
2
C.
-
2
2
≤
m
≤
0...
Đọc tiếp
Tìm giá trị của m để hàm số y = x + m(sinx + cosx + m ) luôn đồng biến trên R
A. - 2 2 ≤ m ≤ 2 2
B. 0 ≤ m ≤ 2 2
C. - 2 2 ≤ m ≤ 0
D. - 2 ≤ m ≤ 2
y ' = 1 + m cos x - sin x = 1 - 2 m sin x - π 4
Đặt t = sin x - π 4 với t ∈ - 1 ; 1 ta có f 1 = 1 - 2 m t
Để hàm số đồng biến trên R thì
f t ≥ 0 ∀ t ∈ - 1 ; 1 ⇔ f - 1 ≥ 0 f 1 ≥ 0 ⇔ 1 + 2 m ≥ 0 1 - 2 m ≥ 0
⇔ m ≥ - 2 2 m ≤ 2 2 ⇔ - 2 2 ≤ m ≤ 2 2
Đáp án A
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của m để hàm số
y
(
m
2
+
m
+
1
)
x
+
(
m
2
-
m
+
1
)
sin
x
luôn đồng biến trên
(
0
;
2
π
)
A.
m
≤
0
B.
m
≥
0
C.
m
0
D.
m...
Đọc tiếp
Tìm tất cả các giá trị thực của m để hàm số y = ( m 2 + m + 1 ) x + ( m 2 - m + 1 ) sin x luôn đồng biến trên ( 0 ; 2 π )
A. m ≤ 0
B. m ≥ 0
C. m > 0
D. m < 0
