Vì n+1 và 2n+1 là số chính phương nên ta đặt n+1=k² và 2n+1=m²     (k,m \(\in\)N)

Ta có: 2n+1 là số lẻ => m² là số lẻ =>m là số lẻ

=>m=2a+1      (a \(\in\) N)

=>m²=(2a+1)²=(2a)²+2.2a.1+1²

                    =4a.a+4.a+1

                  =4a(a+1)+1

=>n=\(\frac{2n-1}{2}=\frac{4a\left(a+1\right)+1-1}{2}=\frac{4a\left(a+1\right)}{2}=2a\left(a+1\right)\)

=>n là số chẵn

=>n+1 là số lẻ => n+1=2b+1              (b \(\in\)N)

=>k²=(2b+1)²=(2b)²+2.2b.1+1²

                    =4b.b+4b+1

                   =4b(b+1)+1

=>n=4b(b+1)+1-1=4b(b+1)

Ta có: b(b+1) là tích 2 số tự nhiên liên tiếp

=>4b(b+1) chia hết cho 2.4=8          (1)

Ta có: k²+m²=(n+1)+(2n+1)=3n+2=2      (mod 3) 

Mà k² chia 3 dư 0 hoặc 1; m² chia 3 dư 0 hoặc 1

=>Để k²+m² =2        (mod 3)

thì k²=1      (mod 3)

và m²=1       (mod 3)

=>m²-k² chia hết cho 3

=>(2n+1)-(n+1)=n chia hết cho 3

Vậy n chia hết cho 3              (2)

Từ (1) và (2) và (8;3)=1

=>n chia hết cho 8.3=24    (đpcm)

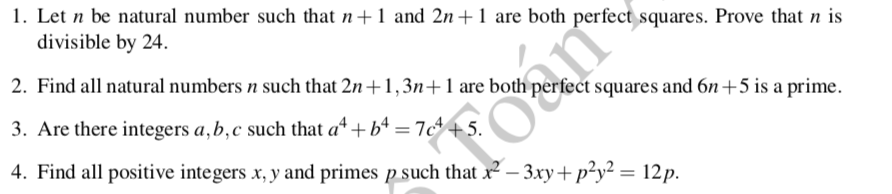
- Chắc là gọi thầy Nguyễn Việt Lâm thôi :)

1.

\(2n+1\) luôn lẻ \(\Rightarrow2n+1=\left(2a+1\right)^2=4a^2+4a+1\Rightarrow n=2a\left(a+1\right)\)

\(\Rightarrow n\) chẵn \(\Rightarrow n+1\) lẻ \(\Rightarrow\) là số chính phương lẻ

\(\Rightarrow n+1=\left(2b+1\right)^2=4b^2+4b+1\)

\(\Rightarrow n=4b\left(b+1\right)\)

Mà \(b\left(b+1\right)\) là tích 2 số tự nhiên liên tiếp \(\Rightarrow\) luôn chẵn

\(\Rightarrow4b\left(b+1\right)⋮8\Rightarrow n⋮8\)

Mặt khác số chính phương chia 3 chỉ có các số dư 0 và 1

Mà \(\left(n+1\right)+\left(2n+1\right)=3n+2\) chia 3 dư 2

\(\Rightarrow n+1\) và \(2n+1\) đều chia 3 dư 1

\(\Rightarrow n⋮3\)

\(\Rightarrow n⋮24\) do 3 và 8 nguyên tố cùng nhau

2.

Lý luận tương tự bài 1, ta được n chẵn

Mặt khác các số chính phương chia 5 chỉ có các số dư 0, 1, 4

Mà: \(\left(2n+1\right)+\left(3n+1\right)=5n+2\) chia 5 dư 2

\(\Rightarrow2n+1\) và \(3n+1\) đều chia 5 dư 1

\(\Rightarrow2n⋮5\Rightarrow n⋮5\) (do 2 và 5 nguyên tố cùng nhau)

\(\Rightarrow n=5k\Rightarrow6n+5=5\left(6k+1\right)\)

- TH1: \(k=0\Rightarrow n=0\Rightarrow6n+5\) là SNT (thỏa mãn)

- TH2: \(k>0\Rightarrow6k+1>0\Rightarrow6n+5\) có 2 ước dương lớn hơn 1 \(\Rightarrow\) không là SNT (loại)

Vậy \(n=0\) là giá trị duy nhất thỏa mãn yêu cầu

Tham khảo:

Nhận xét rằng một số nguyên dương không thể chia 33 dư 22 nên nếu nn không chia hết cho 33 thì một trong hai số n+1,2n+1n+1,2n+1 có một số chia 3 dư 2 nên vô lý. Vậy n⋮3n⋮3. (1)(1)

Có 2n+12n+1 là một chính phương lẻ nên 2n+12n+1 chia 88 dư 11 nên nn chẵn nên n+1n+1 cũng là số chính phương lẻ nên n+1n+1 chia 88 dư 11 nên nn chia hết cho 88. (2)(2)

Từ (1),(2)(1),(2) có n⋮24n⋮24.

Vì 2 n - 1 là số chính phương . Mà 2n - 1 lẻ

\(\Rightarrow2n+1=1\left(mod8\right)\)

=> n \(⋮\) 4

=> n chẵn

=> n+1 cũng là số lẻ

\(\Rightarrow n+1=1\left(mod8\right)\)

=> n \(⋮\) 8

Mặt khác :

\(3n+2=2\left(mod3\right)\)

\(\Rightarrow\left(n+1\right)+\left(2n+1\right)=2\left(mod3\right)\)

Mà n+1 và 2n+1 là các số chính phương lẻ

\(\Rightarrow n+1=2n+1=1\left(mod3\right)\)

=> n chia hết cho 3

Mà ( 3 ; 8 ) = 1

=> n chia hết cho 24

Vì n + 1 và 2n + 1 đêu là phân số chính phương nên đặt n+1 = k\(^2\), 2n+1 = m\(^2\)( k, m \(\in\) N)

Ta có m là số lẻ => m = 2a+1 =>m\(^2\)= 4a(a+1)+1

=>n=\(\frac{m^2-1}{2}\)=\(\frac{4a\left(a+1\right)}{2}\)=2a(a+1)

=> n chẵn =>n+1 là số lẻ =>k lẻ =>Đặt k = 2b+1 (Với b \(\in\) N) =>k\(^2\)=4b(b+1)+1

=> n=4b(b+1) =>n \(⋮\)8 (1)

Ta có k\(^2\) + m\(^2\) =3n+2=2 ( mod3)

Mặt khác k\(^2\) chia 3 dư 0 hoặc 1 ,m\(^2\)chia 3 dư 0 hoặc 1

Nên để k\(^2\)+m\(^2\) =2 (mod3) thì k\(^2\) = 1(mod3)

m\(^2\) = 1 (mod3)

=>m\(^2\)-k\(^2\)\(⋮\)3 hay (2n+1)-(n+1) \(⋮\)3 =>n \(⋮\) 3

Mà (8;3)=1

Từ (1) ; (2) và (3) => n \(⋮\) 24

mod3

Ai làm jup vs ạ

Nhận xét rằng một số nguyên dương không thể chia 33 dư 22 nên nếu nn không chia hết cho 33 thì một trong hai số n+1,2n+1n+1,2n+1 có một số chia 3 dư 2 nên vô lý. Vậy n⋮3n⋮3. (1)(1)

Có 2n+12n+1 là một chính phương lẻ nên 2n+12n+1 chia 88 dư 11 nên nn chẵn nên n+1n+1 cũng là số chính phương lẻ nên n+1n+1 chia 88 dư 11 nên nn chia hết cho 88. (2)(2)

Từ (1),(2)(1),(2) có n⋮24

cuộc đời sao lắm dèm pha 

đi đâu cũng gặp lâu la thế này