VB
Những câu hỏi liên quan
Bài 1: Cho 3 chữ số khác nhau và khác 0. Lập tất cả các số tự nhiên có ba chữ số gồm cả ba chữ số ấy. Chứng minh rằng tổng của chúng chia hết cho 6 và 37.
Bài 2: Có hai số tự nhiên x và y nào mà (x+y) . (x-y) = 1002 hay không?
Bài 3: Tìm các số tự nhiên a và b, sao cho a chia hết cho b và b chia hết cho a.
Cho 5 số tự nhiên khác nhau, biết rẳng tổng ba số bất kỳ luôn lớn hơn tổng hai số còn lại.
a. Chứng minh rằng các số đã cho đều lớn hơn 5
b. tìm tất cả các bộ 5 số trên sao cho tổng các chữ số bé hơn hoặc bằng 40.
Cho ba số tự nhiên khác nhau a, b, c với 0 < a, b, c < 9 . Chứng minh tổng tất cả các số có ba chữ số khác nhau tạo bởi a, b, c chia hết cho 37
Bài 3: Cho ba chữ số: 1,2,4
a) Lập tất cả các số tự nhiên khác nhau, mỗi số có ba chữ số, được viết với đủ ba chữ số đã cho.
b) Tìm tổng của tất cả các số lập được.
a) 124 ; 142 ; 214 ; 241 ; 412 ; 421
b) 124 + 142 + 214 + 241 + 412 + 421 = 1554
Đúng 1
Bình luận (0)
a,A={124;142;214;241;421;412}
b,
124+142+214+241+421+412=1554
Đúng 0
Bình luận (0)
Tìm Tìm tất cả các bộ ba số nguyên tố a, b, c sao cho abc < ab + bc + ca
Vì a, b, c có vai trũ như nhau nên giả sử a ≤ b ≤ c khi đó
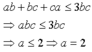
( Vì a là số nguyên tố )
Với a = 2 ta có
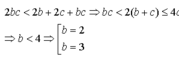
- Nếu b = 2 thì 4c < 2 + 4c thoả món với c là nguyên tố bất kỡ
- Nếu b = 3 thì 6c < 6b + 5c suy ra c < 6 vậy c = 3 hoặc c = 5
Vậy các cạp số (a, b, c) càn Tìm là (2, 2, p) ; (2, 3, 3 ) ; (2, 3, 5 ) và các hoán vị vủa chúng , với p là số nguyên tố .
Đúng 0
Bình luận (0)
Cho tập hợp A = ( 1,2,3,4 )
a) Viết tất cả các tập con của A mà trong các phần tử của nó có đúng một số chẵn.
b) Tìm tất cả các số có ba chữ số khác nhau abc với a b c thuộc A sao cho số đó chia hết cho 3 và 4
a)
đó xong cxaai
từ các chữ số 0 2 5 viết tất cả các số tự nhiên có:
a/ hai chữ số
b/ hai chữ số khác nhau
C/ba chữ số đôi;1 khác nhau
a, 20; 22; 25; 50; 52; 55
b, 20; 25; 50; 52
c, 205; 250; 502; 520
Đúng 2
Bình luận (0)
Tìm ba số tự nhiên khác nhau a ,b,c sao cho abc<ac+bc+ab
abc < ab + bc + ac
<=> 1 < 1/a + 1/b + 1/c (*)
Chỉ có 6 bộ 3 số nguyên tố khác nhau thỏa mãn (*).Đó là (2;3;5); (2;5;3); (3;2;5); (3;5;2); (5;2;3); (5;3;2)
Trả lời : 6 (hoặc 1, nếu xem 6 bộ trên là như nhau)
Đúng 0
Bình luận (0)

