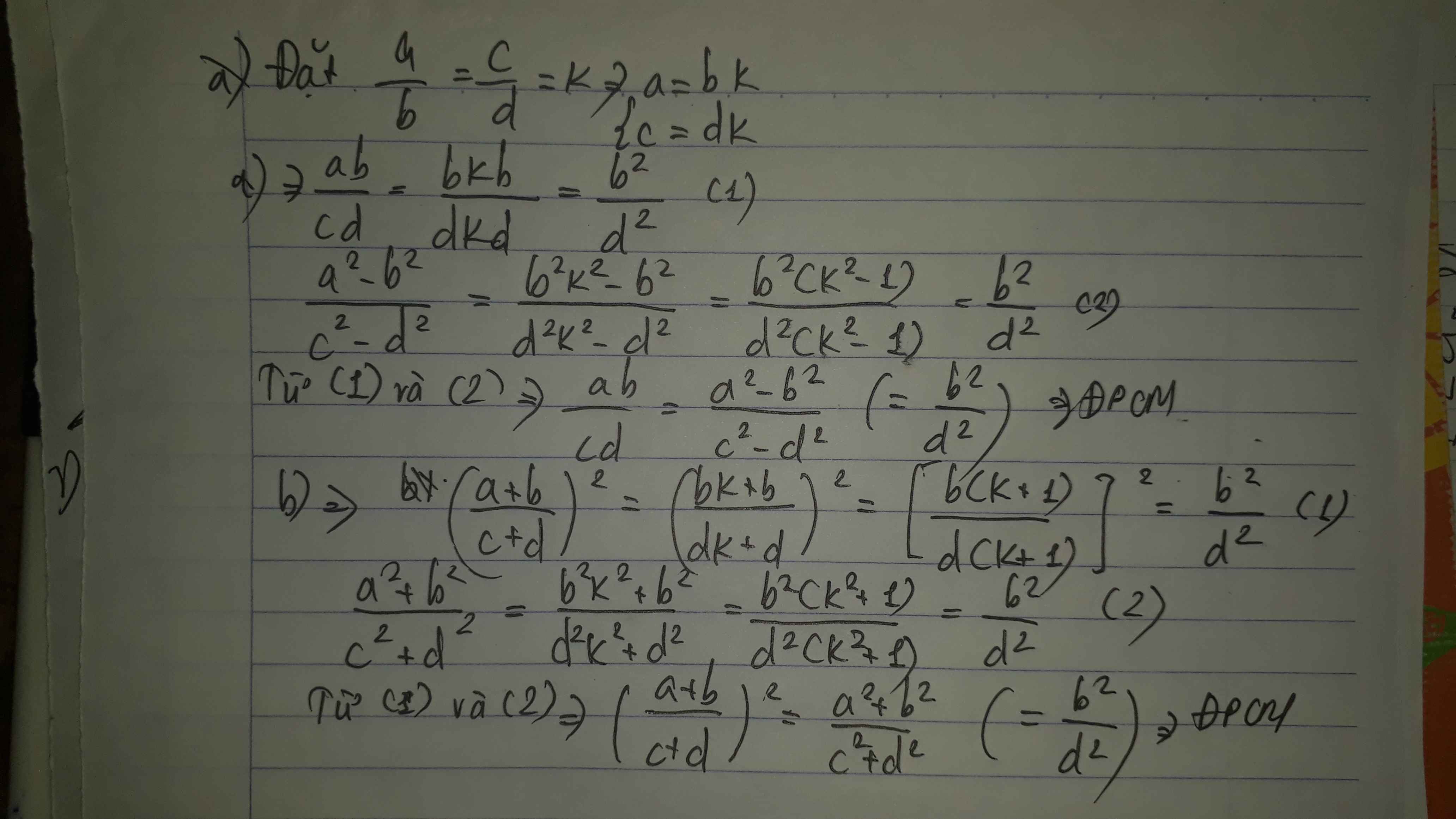Cho tỉ lệ thức . Chứng minh rằng .
GP
Những câu hỏi liên quan
Cho tỉ lệ thức a/b = c/d . Chứng minh rằng ab/cd = ( a - b ) ^ 2 / ( c - d ) ^2
Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=t\Rightarrow a=bt; c=dt$. Ta có:
$\frac{ab}{cd}=\frac{b^2t}{d^2t}=\frac{b^2}{d^2}(1)$
Mặt khác:
$\frac{(a-b)^2}{(c-d)^2}=\frac{(bt-b)^2}{(dt-d)^2}=\frac{b^2(t-1)^2}{d^2(t-1)^2}=\frac{b^2}{d^2}(2)$
Từ $(1); (2)\Rightarrow \frac{ab}{cd}=\frac{(a-b)^2}{(c-d)^2}$
Đúng 0
Bình luận (0)
Cho tỉ lệ thức a^2+b^2/c^2+d^2=ab/cd. Chứng minh rằng a/b=c/d
Cho tỉ lệ thức a^2+b^2/c^2+d^2=ab/cd. Chứng minh rằng a/b=c/d
Đặt
Khi đó ta có :
và
Suy ra :
Ta lại có :
Đúng 1
Bình luận (0)
Đặt
Khi đó ta có :
và
Suy ra :
Ta lại có :
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
cho tỉ lệ thức a^2+b^2/c^2+d^2=ab/cd. chứng minh rằng a/b=c/d
Cho tỉ lệ thức: a/b= c/d. Chứng minh rằng ta có các tỉ lệ thức sau:ab/cd=a^2 - b^2= c^2- d^2
Các bạn giúp mk vs ạ
Ta có \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\Rightarrow\left(\frac{a}{c}\right)^2=\left(\frac{b}{d}\right)^2=\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a.b}{c.d}\left(1\right)\)
Áp dụng tính chất dãy tỉ số bằng nhau tao có
\(\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2-b^2}{c^2-d^2}\left(2\right)\)
Từ (1) và (2) ta có ĐPCM
Đúng 0
Bình luận (0)
\(cho tỉ lệ thức a/b=c/d. chứng minh rằng ab/cd=(a+d)*2 /(c+d)*2\)
dấu *2 là mũ 2 hay là nhân với 2 vậy em ?
Toán lớp mấy đấy,nhìn loằng ngoằng quá
nhân hai anh ơi
Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\) . Chứng minh rằng ta có các tỉ lệ thức sau (giả thiết các tỉ lệ thức là có nghĩa ) :
a) \(\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\)
b) \(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{a^2+b^2}{c^2+d^2}\)
Cho tỉ lệ thức :a^2+b^2/c^2+d^2=ab/cd . Chứng minh rằng: a/b=c/d
(cảm ơn các bạn)
Cho tỉ lệ thức \(\frac{a}{b}=\frac{c}{d}.\) chứng minh rằng ta có các tỉ lệ thức sau (giả thiết các tỉ lệ thức đều có nghĩa)
\(\frac{ab}{cd}=\frac{a^2-b^2}{c^2-d^2}\)
Đặt \(\frac{a}{b}=\frac{c}{d}=k\) thì \(a=bk,c=dk\).
\(\frac{2a+3b}{2a-3b}=\frac{2bk+3b}{2bk-3b}=\frac{b\left(2k+3\right)}{b\left(2k-3\right)}=\frac{2k+3}{2k-3}\\ \frac{2c+3d}{2c-3d}=\frac{2dk+3d}{2dk-3d}=\frac{d\left(2k+3\right)}{d\left(2k-3\right)}=\frac{2k+3}{2k-3}\)
Do đó: \(\frac{2a+3b}{2a-3b}=\frac{2c+3d}{2c-3d}\)
Đúng 0
Bình luận (2)