cho a,b,c là các số thực đôi một khác nhau
NY
Những câu hỏi liên quan
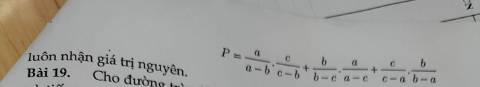
x là số thực và a,b,c là các số thực đôi một khác nhau và khác 0 thỏa mãn \(x=a+\dfrac{1}{b}=b+\dfrac{1}{c}=c+\dfrac{1}{a}\)Tính xabc
cho a,b,c là các số thực khác nhau đôi một và khác 0 thoã mãn:\(a^2-b=b^2-c=c^2-a\)tính gt của P=(a+b)(b+c)(c+a)
Ta có:
\(a^2-b=b^2-c=c^2-a\Rightarrow\hept{\begin{cases}a^2-b^2=b-c\\b^2-c^2=c-a\\c^2-a^2=a-b\end{cases}}\)\(\Rightarrow\hept{\begin{cases}a+b=\frac{b-c}{a-b}\\b+c=\frac{c-a}{b-c}\\c+a=\frac{a-b}{c-a}\end{cases}}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=\frac{b-c}{a-b}.\frac{c-a}{b-c}.\frac{a-b}{c-a}=1\)
Đúng 0
Bình luận (0)
H24
31 tháng 10 2021 lúc 19:43
Cho a, b, c là các số thực dương đôi một khác nhau thỏa mãn:
\(\dfrac{\sqrt{ab}+1}{\sqrt{a}}=\dfrac{\sqrt{bc}+1}{\sqrt{b}}=\dfrac{\sqrt{ca}+1}{\sqrt{c}}\)
Chứng minh rằng abc = 1
Lời giải:
Đổi \((\sqrt{a}, \sqrt{b}, \sqrt{c})=(x,y,z)\) thì bài toán trở thành
Cho $x,y,z$ thực dương phân biệt tm: $\frac{xy+1}{x}=\frac{yz+1}{y}=\frac{xz+1}{z}$
CMR: $xyz=1$
-----------------------------
Có:
$\frac{xy+1}{x}=\frac{yz+1}{y}=\frac{xz+1}{z}$
$\Leftrightarrow y+\frac{1}{x}=z+\frac{1}{y}=x+\frac{1}{z}$
\(\Rightarrow \left\{\begin{matrix} y-z=\frac{x-y}{xy}\\ z-x=\frac{y-z}{yz}\\ x-y=\frac{z-x}{xz}\end{matrix}\right.\)
\(\Rightarrow (y-z)(z-x)(x-y)=\frac{(x-y)(y-z)(z-x)}{x^2y^2z^2}\)
Mà $x,y,z$ đôi một phân biệt nên $(x-y)(y-z)(z-x)\neq 0$
$\Rightarrow 1=\frac{1}{x^2y^2z^2}$
$\Rightarrow x^2y^2z^2=1$
$\Rightarrow xyz=1$ (do $xyz>0$)
Ta có đpcm.
Đúng 3
Bình luận (0)
Chứng minh nếu a; b; c là các số thực đôi một khác nhau thì
\(\frac{a-b}{1+ab}+\frac{b-c}{1+bc}+\frac{c-a}{1+ca}\)khác 0
cho a,b,c là các số thực đôi 1 khác nhau và khác 0 thoả mãn: a^2-b=b^2-c=c^2-a. tính giá thị của biểu thức P=(a+b)(b+c)(c+a)
Cho các số thực a, b, c đôi một khác nhau thỏa mãn a^2-b=b^2-c=c^2-a Chứng minh rằng (a+b+1)(b+c+1)(c+a+1)= -1
Từ \(a^2-b=b^2-c\)
\(\Leftrightarrow\left(a-b\right)\left(a+b\right)=b-c\)
\(\Leftrightarrow a+b=\frac{b-c}{a-b}\)
\(\Rightarrow a+b+1=\frac{b-c}{a-b}+1=\frac{a-c}{a-b}\)
Tương tự ta có:
\(\hept{\begin{cases}b+c+1=\frac{b-a}{b-c}\\c+a+1=\frac{c-b}{c-a}\end{cases}}\)
\(\Rightarrow\left(a+b+1\right)\left(b+c+1\right)\left(c+a+1\right)=\frac{a-c}{a-b}.\frac{b-a}{b-c}.\frac{c-b}{c-a}=-1\)
Đúng 1
Bình luận (0)
cho a,b,c là các số thực thỏa man: a+\(\dfrac{1}{b}=b+\dfrac{1}{c}=c+\dfrac{1}{a\backslash}\).
a) chứng minh nếu a,b,c đôi một khác nhau thì a2b2c2=1
b) chứng minh rằng nếu a,b,c>0 thì a=b=c
cho các số thực a,b,c khác nhau từng đôi một và thỏa mãn điều kiện: a^2-b=b^2-c=c^2-a. CMR: (a+b+1)(b+c+1)(c+a+1)=-1
Ta có: \(a^2-b=b^2-c\Leftrightarrow a^2-b^2=b-c\)
\(\Leftrightarrow\left(a-b\right)\left(a+b\right)=b-c\Rightarrow a+b=\frac{b-c}{a-b}\)
Tương tự CM được: \(b+c=\frac{c-a}{b-c}\) và \(c+a=\frac{a-b}{c-a}\)
Khi đó:
\(\left(a+b+1\right)\left(b+c+1\right)\left(c+a+1\right)\)
\(=\left(\frac{a-b}{c-a}+1\right)\left(\frac{c-a}{b-c}+1\right)\left(\frac{b-c}{a-b}+1\right)\)
\(=\frac{c-b}{c-a}\cdot\frac{b-a}{b-c}\cdot\frac{a-c}{a-b}=-1\)
cho các số thực a,b,c khác nhau từng đôi một và thỏa mãn điều kiện: a^2-b=b^2-c=c^2-a. CMR: (a+b+1)(b+c+1)(c+a+1)=-1
Vì a2 - b = b2 - c = c2 - a
Ta có a2 - b = b2 - c
=> (a - b)(a + b) = b - c
=> a + b + 1 = \(\frac{a-c}{a-b}\)
Tương tự ta có : b + c + 1 = \(\frac{b-a}{b-c}\)
a + c + 1 =\(\frac{b-c}{a-c}\)
Khi đó (a + b + 1)(b + c + 1)(a + c + 1) = \(\frac{a-c}{a-b}.\frac{b-a}{b-c}.\frac{b-c}{a-c}=-1\)(đpcm)