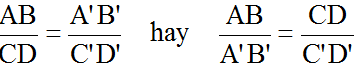phân biệt định lí ta -lét thuận và hệ quả ta-lét
HD
Những câu hỏi liên quan
nêu định lí ta lét, hệ quả định lí ta lét, định lí ta lét đảo
tham khảo
Định lý Talet đảo sẽ được phát biểu như sau: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác. Lưu ý: Định lý vẫn đúng cho trường hợp đường thẳng cắt phần kéo dài hai cạnh của tam giác
Đúng 2
Bình luận (0)
tham khảo
Định lý Talet đảo sẽ được phát biểu như sau: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác. Lưu ý: Định lý vẫn đúng cho trường hợp đường thẳng cắt phần kéo dài hai cạnh của tam giác
Đúng 1
Bình luận (0)
cách phân biệt định lí ta-lét thuận và đảo
mong mọi người giúp mình với ạ
Nếu cho song song =>Talet thuận
Nếu cho tỉ lệ =>Talet đảo
Đúng 1
Bình luận (0)
nêu hệ quả của định lí ta - lét
Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.
Đúng 0
Bình luận (0)
Phát biểu, vẽ hình, ghi giả thiết và kết luận về hệ quả của định lí Ta - lét ?
Định nghĩa: Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A'B' và C'D' nếu có tỉ lệ thức:
Đúng 0
Bình luận (0)
Hệ quả của định lí Talet:
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng với tỉ lệ ba cạnh của tam giác đã cho.
Đúng 0
Bình luận (0)
-Biết MI//BC,viết tỉ lệ thức phù hợp với hệ quả của định lí Ta-lét?-Nếu MI5cm và BC35cm thì tỉ số dfrac{AM}{AB} bằng bao nhiêu? A M I C B
Đọc tiếp
-Biết MI//BC,viết tỉ lệ thức phù hợp với hệ quả của định lí Ta-lét?
-Nếu MI=5cm và BC=35cm thì tỉ số \(\dfrac{AM}{AB}\) bằng bao nhiêu?
a, \(\dfrac{AM}{AB}=\dfrac{MI}{BC};\dfrac{AI}{AC}=\dfrac{MI}{BC};\dfrac{AM}{AB}=\dfrac{AI}{AC}\)
b, Ta có : MI//BC
Theo hệ quả định lý ta-lét ta được
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MI}{BC}=\dfrac{5}{35}=\dfrac{1}{7}\)
Đúng 1
Bình luận (0)
Áp dụng định lí ta - lét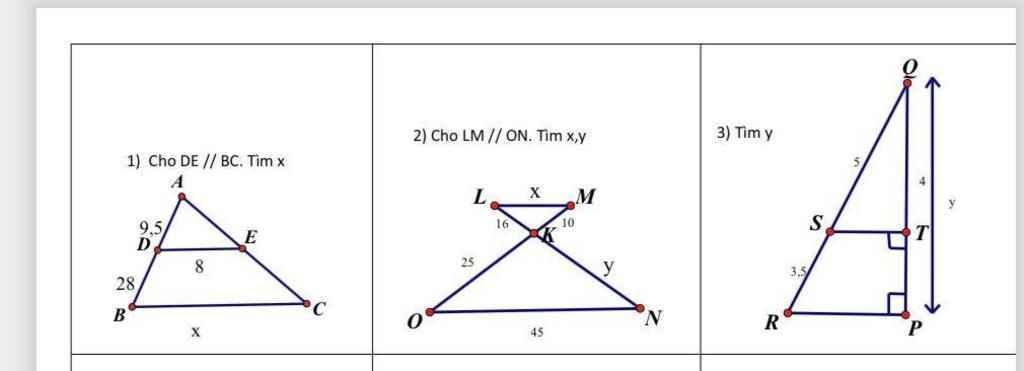
`1).`
Ta có: `AB=AD+DB=9,5+28=37,5`
`\triangle ABC` có: `DE////BC`, theo hệ quả của định lí Ta-lét:
`(AD)/(AB)=(DE)/(BC)`
`=>(9,5)/(37,5)=8/x`
`=>x=(37,5.8)/(9,5)`
`=>x=600/19`
`2).`
`\triangle OKN` có: `LM////ON` theo hệ quả của định lí Ta-lét:
`(KO)/(KM)=(KN)/(KL)=(ON)/(LM)`
`=>25/10=y/16=45/x`
`=>y/16=45/x=5/2`
Với `y/16=5/2=>y=(16.5)/2=40`
Với `45/x=5/2=>x=(45.2)/5=18`
`3).`
Ta có: `ST \bot PQ` và `RP \bot PQ`
`=>ST //// RP`
Có: `QR=QS+SR=5+3,5=8,5`
`(QT)/(QP)=(QS)/(QR)`
`=>4/y=5/(8,5)`
`=>y=(4.8,5)/5`
`=>y=6,8`
`@Nae`
Đúng 2
Bình luận (0)
Baì 1: Nếu quy tắc nhân với 1 số để biến đổi các phương trình
baid 2:Nêu nội dụng định lí ta-lét và ta-lét đảo
bài 3:Giair các phương trình sau:
x+1/3x-1=x+3/3x+2 (/ là phân số nha)
mấy cái đó có trong SGK bạn coi lại đi
Đúng 0
Bình luận (0)
Bài 1:Trong một phương trình,ta có thể nhân cả hai vế với cùng một số khác 0
Bài 2:+,Định lí Ta-lét:Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ
+,Định lí Ta-lét đảo:Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác
Bài 3:
\(\frac{x+1}{3x-1}=\frac{x+3}{3x+2}\)
\(\Leftrightarrow\frac{x+1}{3x-1}-\frac{x+3}{3x+2}=0\)
\(\Leftrightarrow\frac{\left(x+1\right)\left(3x+2\right)}{\left(3x-1\right)\left(3x+2\right)}-\frac{\left(x+3\right)\left(3x-1\right)}{\left(3x-1\right)\left(3x+2\right)}=0\)
\(\Leftrightarrow\frac{3x^2+2x+3x+2}{\left(3x-1\right)\left(3x+2\right)}-\frac{3x^2-x+9x-3}{\left(3x-1\right)\left(3x+2\right)}=0\)
\(\Leftrightarrow3x^2+5x+2-3x^2+8x-3=0\)
\(\Leftrightarrow13x-1=0\)
\(\Leftrightarrow13x=1\)
\(\Leftrightarrow x=\frac{1}{13}\)
Vậy tập nghiệm của phương trình là \(S=\left\{\frac{1}{13}\right\}\)
Đúng 0
Bình luận (0)
Phát biểu định lí Ta – lét trong không gian.
Định lí Ta – lét trong không gian:
- Định lí thuận (Định lí Ta – lét)
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì các đoạn thẳng tương ứng tỉ lệ, nghĩa là:
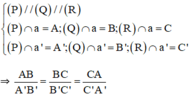
Định lí đảo (Định lí Ta – lét đảo)
Giả sử trên hai đường thẳng a và a' lần lượt lấy hai bộ ba điểm (A, B, C) và (A', B', C') sao cho AB/A'B'= BC/B'C' = CA/C'A'
Khi đó ba đường thẳng AA', BB', CC' cùng song song với một mặt phẳng, nghĩa là ba đường thẳng đó nằm trên ba mặt phẳng song song với nhau.
Đúng 0
Bình luận (0)
hãy giúp minh nêu định lí ta-lét
Định lý Ta-lét:
Nếu một dường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại của nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
-Chúc bạn học tốt.
Đúng 0
Bình luận (0)
định lí ta-lét?
TL:
Định nghĩa : Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
Đúng 0
Bình luận (0)
Định lý Talet thuận trong tam giác
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
hok tốt
Đúng 0
Bình luận (0)