Cho tam giác ABC vẽ tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số đồng dạng là K = 2/3.
NQ
Những câu hỏi liên quan
Biết tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số đồng dạng k = 4/5 . Khi đó tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số đồng dạng là:
A. 5 4
B. 4 5
C. 1 5
D. 3 4
Cho tam giác ABC và tam giác A’B’C’ đồng dạng với nhau theo tỉ số k. a,Tìm tỉ số 2 đường cao tương ứng AH/A’H’ theo k b,Tìm tỉ số diện tích của tam giác ABC và tam giác A’B’C’ theo k
b) Ta có: ΔABC\(\sim\)ΔA'B'C'(gt)
nên \(\dfrac{S_{ABC}}{S_{A'B'C'}}=\left(\dfrac{AB}{A'B'}\right)^2\)(Định lí tỉ số diện tích của hai tam giác đồng dạng)
hay \(\dfrac{S_{ABC}}{S_{A'B'C'}}=k^2\)
Đúng 1
Bình luận (0)
Cho tam giác ABC đồng dạng với tam giác A’B’C’ tỉ số đồng dạng là 1/2 biết AB=3cm AC=4cm BC=5cm
a) tính các cạnh của tam giác A’B’C’
b) vẽ MN song song với B’C’ . Chứng minh tam giác ABC đồng dạng với tam giác A’MN
c) Biết A’M=4cm. Tính A’M; MN
d) kẻ A’H vuông góc với B’C’; A’H cắt MN tại K. Tính A’H và A’K
Cho tam giác A’B’C’ có A’E’ là đường phân giác và tam giác ABC có AE là đường phân giác.Biết tam giác A’B’C’ ~ tam giác ABC theo tỉ số đồng dạng k. CM A’E’/ AE=k
ΔA'B'C' đồng dạng với ΔABC
=>A'B'/AB=B'C'/BC=A'C'/AC=k và góc A'=góc A; góc B=góc B' góc C'=góc C
=>góc BAE=góc B'A'E'
Xét ΔABE và ΔA'B'E' có
góc B=góc B'
góc BAE=góc B'A'E'
=>ΔABE đồng dạng với ΔA'B'E'
=>AE/A'E'=AB/A'B'
=>A'E'/AE=A'B'/AB=k
Đúng 0
Bình luận (0)
Cho tam giác ABC, vẽ tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số đồng dạng k = 2/3.
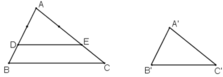
+ Dựng ΔADE 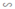 ΔABC theo tỉ số 2/3
ΔABC theo tỉ số 2/3
Trên AB lấy D, trên AC lấy E sao cho 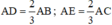
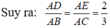
Khi đó theo định lý Ta-let đảo ta suy ra DE // BC
⇒ ΔADE 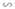 ΔABC theo tỉ số 2/3.
ΔABC theo tỉ số 2/3.
+ Dựng ΔA’B’C’ = ΔADE
Vẽ đoạn A’B’ = AD.
Dựng góc 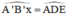
Trên tia B’x lấy điểm C’ sao cho B’C’ = DE.
Nối C’A’ ta được ΔA’B’C’ = ΔADE (c.g.c)
Suy ra: ΔA’B’C’ đồng dạng với ΔADE theo tỉ số:
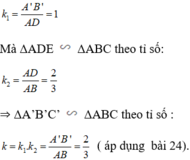
Đúng 0
Bình luận (0)
Cho ABC có AB=6cm; AC=8cm, BC=12cm. Tam giác A’B’C’ đồng dạng với tam giác ABC với tỉ số đồng dạng là 3/2.
a) Tính độ dài các cạnh của tam giác A’B’C’
b) Tính tỉ số chu vi của hai tam giác trên
a: Ta có: ΔA'B'C'∼ΔABC
nên A'B'/AB=B'C'/BC=A'C'/AC
=>A'B'/6=B'C'/12=A'C'/8=3/2
=>A'B'=9cm; B'C'=18cm; A'C'=12cm
b: Ta có: ΔA'B'C'∼ΔABC
nên \(\dfrac{C_{A'B'C'}}{C_{ABC}}=\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
Hãy chọn câu trả lời đúng. Nếu tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số k thì tỉ số chu vi của tam giác A’B’C’ và ABC bằng
A. 1
B. 1 k
C. k
D. k 2
Vì tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số k nên A B A ' B ' = A C A ' C ' = B C B ' C ' = k
Suy ra A ' B ' A B = A ' C ' A C = B ' C ' B C = 1 k
Áp dụng tính chất dãy tỉ số bằng nhau ta có
A ' B ' A B = A ' C ' A C = B ' C ' B C = A ' B ' + A ' C ' + B ' C ' A B + A C + B C = 1 k
Vậy tỉ số chu vi của tam giác A’B’C’ và ABC là 1 k
Đáp án: B
Đúng 0
Bình luận (0)
cho tam giác abc đồng dạng với tam giác khg theo tỉ số 2:3 và tam giác khg đồng dạng với tam giác mnp theo tỉ số 1:3 vậy tam giác abc đồng dạng với tam giác mnp theo tỉ số nào
a)k=3:9. b) k=2:9. c) k=2:6 d) k=1:3
Cho tam giác \(ABC\), hãy vẽ một tam giác đồng dạng với tam giác \(ABC\) theo tỉ số đồng dạng \(k = \frac{1}{2}\).
Bước 1: Vẽ tam giác \(ABC\) bất kì.
Bước 2: Gọi \(M\) là trung điểm của \(AB\), \(N\) là trung điểm của \(AC\).
Khi đó ta có \(\Delta AMN\backsim\Delta ABC\) theo tỉ số \(k = \frac{1}{2}\).
Chứng minh:
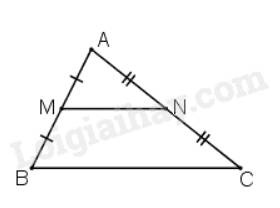
Vì \(M\) là trung điểm của \(AB\), \(N\) là trung điểm của \(AC\) nên \(MN\) là đường trung bình của tam giác \(ABC\)\( \Rightarrow \left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right.\).
Ta có \(MN//BC\) và \(M,N\) cắt \(AB,AC\) tại \(M,N\) nên \(\Delta AMN\backsim\Delta ABC\) (định lí).
Khi đó, \(\frac{{MN}}{{BC}} = \frac{1}{2}\)
Đúng 0
Bình luận (0)



