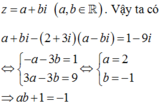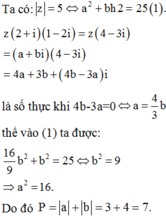tìm a,b ϵ N thỏa mãn: 10↑a + 168 =b↑2
LL
Những câu hỏi liên quan
1) Cho a,b ϵ N thỏa mãn 3a+8b⋮3
Chứng tỏ a, -a + 26 ⋮ 3
b, 10.a+b⋮3
c, a+16b ⋮ 3
tìm x , y thỏa mãn :
a . 2x + 124 = 5y
b . 10x + 168 = y2
a) 2x + 124 = 5y
Ta thấy : 5y luôn lẻ (\(\forall\)y) => 2x + 124 cũng là số lẽ
Mà 124 là số chẵn => 2x là số lẽ => x = 0
Với x = 0 => 20 + 124 = 5y
=> 1 + 124 = 5y
=> 125 = 5y
=> 5y = 53
=> y = 3
Vậy x = 0; y = 3 thõa mãn
b) Ta có: 10x + 168 = y2
=> 10x = y2 - 168
+) Nếu y là số lẻ => y2 là số lẻ
=> y2 - 168 lẻ
=> 10x lẻ => x = 0
Với x = 0 => 100 + 168 = y2
=> 1 + 168 = y2 => 169 = y2
=> y2 = 132
=> \(\orbr{\begin{cases}y=13\\y=-13\end{cases}}\)
+) Nếu y chẵn => y2 chẵn
=> y2 - 168 chẵn
=> 10x chẵn
Do 10x \(⋮\) 10 => y2 - 168 \(⋮\)10
Mà y2 là số chính phương (ko có tận cùng là 8)
=> y2 - 168 ko \(⋮\) 10
=> pt vô nghiệm
Vậy x = 0 và y = 13 hoặc x - 0 và y = -13 thõa mãn
Đúng 0
Bình luận (0)
Xét đề bài là tìm x y là số tự nhiên
a) \(2^x+124=5^y\)
+) Với x=0
ta có:
\(2^0+124=5^y\)
\(5^y=125=5^3\)
y=3
+) Với x>0 => y>3
Ta có: \(2^x+124⋮2\)
và \(5^y\) không chia hết cho 2
=> phương trình vô nghiệm
Vậy x=0; y=3
b) \(10^x+168=y^2\)
+) Với x=0 thay vào ta có:
\(y^2=169=13^2\Rightarrow y=13\)
+) Với x>0 => y>13
\(10^x+168=y^2\)
Ta có VT chia 10 dư 8
VP là số chính phương chia 10 không thể dư 8 được
=> phương trình vô nghiệm
Vậy x=0 và y=13 thỏa mãn
Đúng 0
Bình luận (0)
2x + 124 = 5y
Ta có : 5y là số lẻ mà 124 và 2x là số chẵn => x ; y không thoả mãn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho a,b,c ϵ R thỏa mãn a≥1; b≥1; 0≤c≤1 và a+b+c=3. Tìm GTLN và GTNN của P = (a2+b2+c2)/ab+bc+ca
\(P=\dfrac{a^2+b^2+c^2}{ab+bc+ca}\ge\dfrac{ab+bc+ca}{ab+bc+ca}=1\)
\(P_{min}=1\) khi \(a=b=c=1\)
\(P=\dfrac{\left(a+b+c\right)^2-2\left(ab+bc+ca\right)}{ab+bc+ca}=\dfrac{9}{ab+bc+ca}-2\)
Do \(a;b\ge1\Rightarrow\left(a-1\right)\left(b-1\right)\ge0\Rightarrow ab\ge a+b-1=2-c\)
\(\Rightarrow ab+c\left(a+b\right)\ge2-c+c\left(3-c\right)=-c^2+2c+2=c\left(2-c\right)+2\ge2\)
\(\Rightarrow P\le\dfrac{9}{2}-2=\dfrac{5}{2}\)
\(P_{max}=\dfrac{5}{2}\) khi \(\left(a;b;c\right)=\left(1;2;0\right);\left(2;1;0\right)\)
Đúng 0
Bình luận (0)
Vẽ các đường thẳng a,b và các điểm A,B,C thỏa mãn điều kiện sau:
a) A ϵ b ; b) C ko thuộc a và ( ko thuộc b,c) c) B ϵ a và B ϵ b
Cho số phức z a+bi(a,b ϵ ℝ) thỏa mãn
2
z
-
5
z
-
-
9
-
14
i
Tính S a + b A. S -1 B. S 1 C. S -23/3 D. S 23/3
Đọc tiếp
Cho số phức z =a+bi(a,b ϵ ℝ) thỏa mãn 2 z - 5 z - = - 9 - 14 i
Tính S =a + b
A. S= -1
B. S= 1
C. S= -23/3
D. S= 23/3
Cho số phức za+bi (a,b ϵ ℝ) thỏa mãn :
z
-
2
+
3
i
z
-
1
-
9
i
. Giá trị của ab+1 là : A. 1. B. -2. C. -1. D. 0.
Đọc tiếp
Cho số phức z=a+bi (a,b ϵ ℝ) thỏa mãn : z - 2 + 3 i z - = 1 - 9 i . Giá trị của ab+1 là :
A. 1.
B. -2.
C. -1.
D. 0.
Cho số phức z = a+bi(a,b ϵ ℝ) thỏa mãn |z|=5z và z(2+i)(1-2i) là một số thực. Tính giá trị P=|a|+|b|
A.P=8
B.P=4
C.P=5
D. P=7
Cho tứ giác ABCD, AC vuông góc với BD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. CMR: MP= NQ
Bài 8: Cho a, b thuộc R thỏa mãn: a+ b+ab=8. Tìm GTNN của B= a^2+b^2
Bài 9: Cho a, b thuộc R thỏa mãn: a+b+ab=35. Tìm GTNN của: C= a^2+b^2
Bài 10: Tìm n để: (n thuộc N)
a) n^2+5
b) n^2-n+1 là số chính phương
a) Tìm số tự nhiên a,b thỏa mãn 10 mũ a+483=b mũ 2
b) Tìm các số tự nhiên a, b,c thỏa mãn: a mũ 2+ab+ác=20×ab+b mũ 2+BC=180×ac+BC+c mũ 2=200
a) \(10^a+483=b^2\) (*)
Nếu \(a=0\) thì (*) \(\Leftrightarrow b^2=484\Leftrightarrow b=22\)
Nếu \(a\ge1\) thì VT (*) chia 10 dư 3, mà \(VP=b^2\) không thể chia 10 dư 3 nên ta có mâu thuẫn. Vậy \(\left(a,b\right)=\left(0,22\right)\) là cặp số tự nhiên duy nhất thỏa mãn điều kiện bài toán.
(Chú ý: Trong lời giải đã sử dụng tính chất sau của số chính phương: Các số chính phương khi chia cho 10 thì không thể dư 2, 3, 7, 8. Nói cách khác, một số chính phương không thể có chữ số tận cùng là 2, 3, 7, 8)
b) Bạn gõ lại đề bài nhé, chứ mình nhìn không ra :))
Đúng 0
Bình luận (0)