Cho tam giác ABC có AB=9cm, AC=16cm, BC=20cm. Chứng minh rằng góc B = 1/2 góc A
BT
Những câu hỏi liên quan
câu 1 Cho tam giác ABC có các góc B, C nhọn. Kẻ AH vuông góc với BC. Biết AB = 20cm, BH = 16cm, HC = 5cm. Tính AH, AC.
câu 2 Cho tam giác ABC có các góc B, C nhọn. Kẻ AH vuông góc với BC, biết AC = 15cm, HB = 5cm, HC = 9cm . Tính độ dài cạnh AB.
Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm
Đúng 1
Bình luận (0)
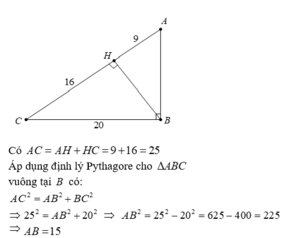
Cho tam giác ABC vuông ở A có AC=20cm. Kẻ AH vuông góc BC. Biết BH=9cm;HC=16cm. Tính AB,AH
A. AH=12cm;AB=15cm
B. AH=10cm;AB=15cm
C. AH=15cm;AB=12cm
D. AH=12cm;AB=13cm
Lg
*Áp dụng định lý py-ta-go ta có: (Δ AHC)
AC2=AH2+HC2
202=AH2+162
400=AH2+256
AH2=144
AH=√144 =12
*Áp dụng định lý py-ta-go ta có: (Δ AHB)
AB2=AH2+BH2
AB2=122+92
AB2=225
AB=√225 =15
Đúng 0
Bình luận (0)
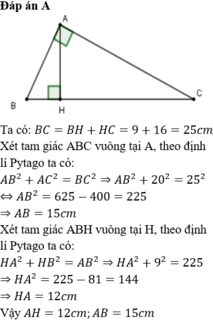
Cho tam giác ABC có CB = 20cm . Kẻ BH vuông góc với AC , biết AH = 9cm , HC = 16cm . Chứng minh tam giác ABC là tam giác vuông.
Xét △BHC vuông tại H có: BH2 + HC2 = BC2 (định lý Pytago)
=> BH2 + 162 = 202
=> BH2 = 202 - 162 = 400 - 256 = 144
=> BH = 12 (cm)
Xét △BHA vuông tại H có: BH2 + AH2 = AB2 (định lý Pytago)
=> 122 + 92 = AB2
=> AB2 = 144 + 81 = 225
=> AB = 15 (cm)
Ta có: AC = AH + HC = 9 + 16 = 25
Xét △ABC có:
AC2 = 252 = 625
AB2 + BC2 = 152 + 202 = 225 + 400 = 625
=> AC2 = AB2 + AC2
=> △ABC vuông tại A
Cho tam giác ABC có AB=12cm, BC=16cm, AC=20cm.
a, Hỏi tam giác ABC vuông tại đâu?
b, Kẻ BH vuông góc với AC tại H. BM là phân giác góc HBA ( M thuộc HA). Chứng minh góc CBM cân.
Cho tam giác ABC có AB=AC=10cm; BC=16cm. Trung tuyến AM. Chứng Minh rằng : A) Tam giác ABM= Tam giác AC B) AM vuông góc BC C) Tính độ dài AM
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: BM=CM=BC/2=8(cm)
nên AM=6(cm)
Đúng 5
Bình luận (1)
tham khảo
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: BM=CM=BC/2=8(cm)
nên AM=6(cm)
Đúng 3
Bình luận (0)
a, Ta có :
AB = AC (gt)
=> Δ ABC cân tại A
Xét Δ ABM và Δ ACM, có :
AB = AC (gt)
MB = MC (M là trung điểm BC)
\(\widehat{ABM}=\widehat{ACM}\) (Δ ABC cân tại A)
=> Δ ABM = Δ ACM
b, Ta có :
AM là đường trung tuyến
Δ ABC cân tại A
=> AM ⊥ BC
c, Ta có :
BC = 2MB
=> 16 = 2MB
=> MB = 8 (cm)
Xét Δ AMB vuông tại M, có :
\(AB^2=AM^2+BM^2\)
=> \(10^2=AM^2+8^2\)
=> \(AM^2=36\)
=> AM = 6 (cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại B. Kẻ BH vuông góc với AC. Biết BC = 20cm, HA = 9cm, HC = 16cm. Hãy tính AB bằng hai cách
Bài 5. Cho tam giác ABC có AB= 12cm, AC= 16cm, BC= 20cm. Gọi D là trung điểm của BC. Qua D kẻ
đường thẳng vuông góc với BC cắt AB và AC lần lượt tại M và N.
a/ Chứng minh tam giác DNC đồng dạng tam giác ABC.
b/ Tính các cạnh của tam giác DNC.
c/ Tính MB, MC
a, Ta có:\(AB^2+AC^2=12^2+16^2=400\)(cm)
\(BC^2=20^2=400\)(cm)
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A
Xét Δ DNC và Δ ABC có:
\(\widehat{NDC}=\widehat{BAC}\left(=90^o\right)\)
Chung \(\widehat{C}\)
⇒Δ DNC \(\sim\) Δ ABC (g.g)
b, Ta có: BD=DC=1/2.BC=1/2.20=10(cm)
Δ DNC \(\sim\) Δ ABC (cma)
\(\Rightarrow\dfrac{ND}{AB}=\dfrac{NC}{BC}=\dfrac{DC}{AC}\Rightarrow\dfrac{ND}{12}=\dfrac{NC}{20}=\dfrac{10}{16}\Rightarrow\left\{{}\begin{matrix}ND=7,5\left(cm\right)\\NC=12,5\left(cm\right)\end{matrix}\right.\)
c, Xét Δ DBM và Δ ABC có:
Chung \(\widehat{B}\)
\(\widehat{BDM}=\widehat{BAC}\left(=90^o\right)\)
⇒Δ DBM \(\sim\) Δ ABC(g.g)
\(\Rightarrow\dfrac{MB}{BC}=\dfrac{BD}{AB}\Rightarrow\dfrac{MB}{20}=\dfrac{10}{12}\Rightarrow MB=\dfrac{50}{3}\left(cm\right)\)
Ta có: MD⊥BC, BD=DC ⇒ ΔBDC cân tại M
\(\Rightarrow MB=MC=\dfrac{50}{3}\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC có cạnh AB = 12cm, AC = 16cm, BC = 20cm. Kẻ đường cao AM. Kẻ ME vuông góc với AB.
a) Chứng minh tam giác ABC là tam giác vuông.
b) Tính độ dài AM, BM.
c) Chứng minh AE.AB = AC2 – MC2.
d) Chứng minh AE . AB = MB . MC = EM . AC.
a, Vì \(BC^2=400=256+144=AC^2+AB^2\) nên tam giác ABC vuông tại A
b, Áp dụng HTL: \(AM=\dfrac{AB\cdot AC}{BC}=9,6\left(cm\right)\)
\(BM=\dfrac{AB^2}{BC}=7,2 \left(cm\right)\)
c, Áp dụng HTL: \(AE\cdot AB=AM^2\)
Áp dụng PTG: \(AM^2=AC^2-MC^2\)
Vậy \(AE\cdot AB=AC^2-MC^2\)
d, Áp dụng HTL: \(AE\cdot AB=MB\cdot MC=AM^2\)
\(\left\{{}\begin{matrix}\widehat{EAM}=\widehat{ACM}\left(cùng.phụ.\widehat{MAC}\right)\\\widehat{AEM}=\widehat{AMC}=90^0\end{matrix}\right.\Rightarrow\Delta AEM\sim\Delta CMA\left(g.g\right)\\ \Rightarrow EM\cdot AC=AM^2\)
Vậy ta được đpcm
Đúng 1
Bình luận (0)
Cho tam giác ABC, có AB = 16cm; BC = 20cm; AC = 12cm.
a) Chứng min : ∆ABC vuông tại A
b) Gọi M là trung điểm của BC. Kẻ MF vuông góc với AC tại F. Chứng minh : FA = FC
c) Gọi E là trung điểm của AB. Chứng minh : ME vuông góc AB và tính độ dài của ME
MK vẽ hình ko chính xac lam bn thông cảm hen!!!
a) Xét ΔABC,có: AB2 + AC2 = 162 + 122 = 400
BC2 = 202 = 400
Do đó AB2 + AC2 = BC2
Theo ĐL Pytago đảo, ΔABC vuông tại A
b) Do AB vuông góc AC
MF vuông góc AC
Nên MF // AB
Xét ΔABC có: MB=MC(gt)
MF// AB(cm trên)
Suy ra MF là đường TB của ΔABC
=> F là trung điểm AC
Vậy FA=FC(đpcm)
c) Xét ΔABC có : MB = MC(gt)
MA = ME (gt)
Nên ME là đường TB của ΔABC
=> ME // AC ; ME =\(\frac{1}{2}\)AC
Mà AC vuông góc AB (cm trên)
Vậy ME vuông góc với AB
Do AC= 12 cm (gt)
Nên ME = 1/2 AC = 12/2= 6cm
Vậy ME= 6cm.
Đúng 1
Bình luận (0)