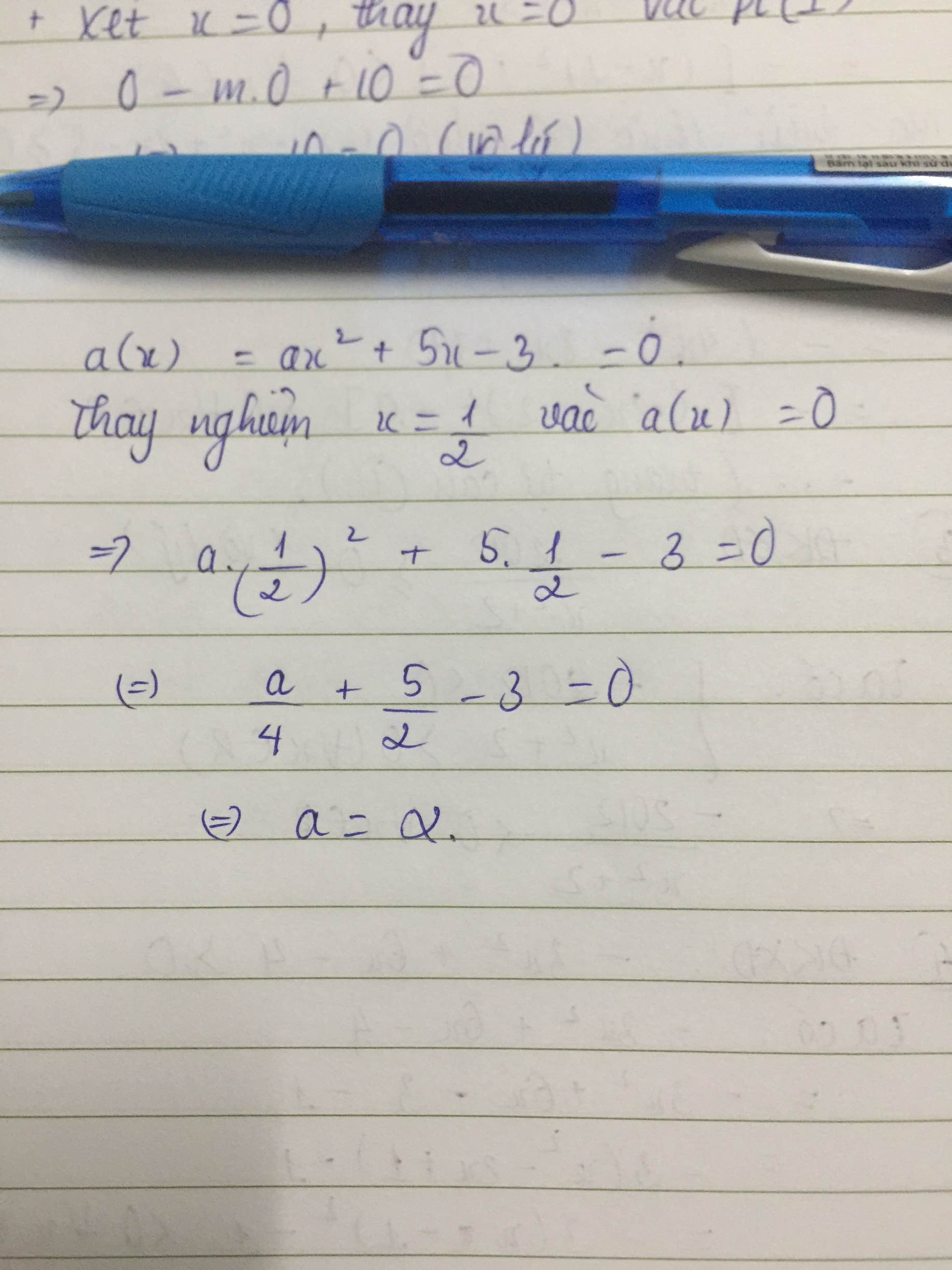thay x=1/2 đc a/4+5/2-3=0 =>a=2

Thay \(x=\dfrac{1}{2}\) vào đa thức a(x), ta được:

\(a\cdot\dfrac{1}{4}+\dfrac{5}{4}-3=0\)

\(\Leftrightarrow\dfrac{1}{4}a=\dfrac{7}{4}\)

hay a=7

Ta có P(0,5)=0

=>a0,5^2+5.0,5-3=0

=>0,25a+2,5-3=0

=>0,25a-0,5=0

=>0,25a=0,5

=>a=0,5-0,25

a=0,25

Vậy hệ số a là 0,25

P(x) = ax² + 5x - 3

Đa thức này có một nghiệm là 1/2 tức là P(1/2) = 0

=> a/4 + 5/2 - 3 = 0

=> a = 2

Đáp số: a = 2

P(x) = ax^2 + 5x - 3
Đa thức này có một nghiệm là 1/2 tức là P(1/2) = 0
=> a/4 + 5/2 - 3 = 0
=> a = 2
Đáp số: a = 2

Ta có : \(h\left(\frac{3}{2}\right)=a\left(\frac{3}{2}\right)^2-5.\frac{3}{2}+3=0\)

\(\Leftrightarrow\frac{9a}{4}-\frac{15}{2}+3=0\)

\(\Leftrightarrow\frac{9a}{4}-\frac{30}{4}+\frac{12}{4}=0\)

Khử mẫu ta đc : \(9a-30+12=0\)

\(\Leftrightarrow9a=18\Leftrightarrow a=2\)

Nghiệm của đa thức M(x) là \(\dfrac{1}{2}\)

\(\Rightarrow x=\dfrac{1}{2}\) để đa thức M(x) = 0

Thay \(x=\dfrac{1}{2}\), ta có:

\(a.\left(\dfrac{1}{2}\right)^2+5.\dfrac{1}{2}-3=0\\ \Rightarrow\dfrac{1}{4}a+\dfrac{5}{2}=3\\ \Rightarrow\dfrac{1}{4}a=3-\dfrac{5}{2}\\ \Rightarrow\dfrac{1}{4}a=\dfrac{1}{2}\\ \Rightarrow a=\dfrac{1}{2}:\dfrac{1}{4}=2\)

Vậy a = 2. Đa thức M(x) được viết đầy đủ dưới dạng:

\(M\left(x\right)=2x^2+5x-3\)

M(x) có nghiệm là 1/2 nên khi x = 1/2 thì M(x) = 0

\(a\left(\dfrac{1}{2}\right)^2+5.\dfrac{1}{2}-3=0\)

\(\Rightarrow a=2\)

Vậy...

P(x) = ax^2 + 5x - 3
Đa thức này có một nghiệm là 1/2 tức là P(1/2) = 0
=> a/4 + 5/2 - 3 = 0
=> a = 2
Đáp số: a = 2

c=1/3xy².(-3/4yz)

dễ mà bạn

a) Ta có f(7) = a7 + b và f(2) + f(3) = (a2+ b) + (a3 + b) = 5a + 2b. Vậy để f(7) = f(2) + f(3), ta cần giải phương trình:
a7 + b = 5a + 2b
Simplifying, ta được: 2a = b.
Vậy điều kiện của a và b để f(7) = f(2) + f(3) là b = 2a.
b) Để tìm nghiệm của P(x), ta cần giải phương trình (x-2)(2x+5) = 0:
(x-2)(2x+5)= 0
→ X-2 = 0 hoặc 2x+5 = 0
→ x = 2 hoặc x = -5/2
Vậy nghiệm của P(x) là x = 2 hoặc x =-5/2.
c) Ta biết rằng đa thức P(x) có 1 nghiệm là -2, vậy ta có thể viết P(x)

dưới dạng:
P(x) = (x+2)(x^3 - 2x^2 + ax - 2)
Từ đó suy ra:
P(-2) = (-2+2)(8 - 4a - 2) = 0
⇔-8a= 16
⇔a = -2
Vậy hệ số a của P(x) là -2.

tại sao a7 + b = 5a + 2b lại bằng  2a = b vậy ạ

Thay x =\(\frac{1}{2}\)vào đa thức M(x) ta có :

M(x) = a . \(\left(\frac{1}{2}\right)^2\) + 5 . \(\frac{1}{2}\) - 3

=> M(x) = a . \(\frac{1}{4}\)- \(\frac{1}{2}\)

=> M(x) = \(\frac{1}{4}\)a - \(\frac{1}{2}\)

Cho \(\frac{1}{4}\)a - \(\frac{1}{2}\) = 0

=> \(\frac{1}{4}\)a = \(\frac{1}{2}\)

=> a = 2

Vậy hệ số a = 2.

h(x) có nghiệm là 3/2
=> h(3/2) = a*(3/2)^2 -5*3/2 +3
                => a*(9/4) -15/2 +3 =0
                     a(9/4) =15/2-3
                        a= (9/2) :(9/4)
                        a = 2