Chứng minh rằng các phương trình sau tương đương:
2x = 6 và 1,5x = 4,5
Chứng minh rằng các phương trình sau tương đương 2x = 6 và 1,5x = 4,5.
Ta có:
+ Phương trình 2x = 6 ⇔ x = 3 có tập nghiệm là S = { 3 }
+ Phương trình 1,5x = 4,5 ⇔ x = 4,5/1,5 ⇔ x = 3 có tập nghiệm là S = { 3 }
→ Hai phương trình có cùng tập nghiệm.
→ Hai phương trình tương đương.
Chứng minh rằng các phương trình sau tương đương - 2 x = 4 và x 2 = - 1
Ta có:
+ Phương trình - 2x = 4 ⇔ x = - 2 có tập nghiệm là S = {- 2}
+ Phương trình x/2 = - 1 ⇔ x = - 2 có tập nghiệm là S = {- 2}
→ Hai phương trình có cùng tập nghiệm.
→ Hai phương trình tương đương.
Chứng minh hai bất phương trình sau không tương đương 2x + 1 > 3 và |x| > 1
Giải bất phương trình 2x + 1 > 3 ta tìm được tập nghiệm là x > 1
Ta kiểm tra được x = -2 là nghiệm của bất phương trình |x| > 1 nhưng không là nghiệm của 2x + 1 > 3 (không thuộc tập nghiệm x > 1)
Vậy hai bất phương trình 2x + 1 > 3 và |x| > 1 không tương đương.
Xét xem các phương trình sau có tương đương không? 2x - 6 = 0 và x(x - 3) = 0
Phương trình 2x – 6 = 0 ⇔ 2x = 6 ⇔ x = 3
⇒ phương trình 2x – 6 = 0 có tập nghiệm S = {3}
Phương trình x(x – 3) = 0 có tập nghiệm S = {0;3}
Vậy 2 phương trình 2x - 6 = 0 và x(x - 3) = 0 không tương đương
Tìm xy biết xy+2x-5y=0( x, y thuộc Z)
Tìm m để hai phương trình sau tương đương: 2x^2-8x+15=0 và (2x-6)(mx-3m+1)=0
chứng minh phương trình a(x-a^2+1)=a^2+2-2x luôn có nghiệm dương với a khác -2
Tìm xy biết xy+2x-5y=0( x, y thuộc Z)
\(\Rightarrow x(y+2)-5(y+2)=-10\)
\(\Rightarrow(x-5)(y+2)=-10\)
Vì \(x,y\in Z\Rightarrow x-5,y+2\in Z\)
Ta có bảng sau:
| x-5 | 1 | -1 | -2 | -5 | 2 | 5 | 10 | -10 |
| y+2 | -10 | 10 | 5 | 2 | -5 | -2 | -1 | 1 |
| x | 6 | 4 | 3 | 0 | 7 | 10 | 15 | -5 |
| y | -12 | 8 | 3 | 0 | -7 | -4 | -3 | -1 |
Chúc bạn học tốt!
Chứng minh hai phương trình 1 2 ( x - 3 ) = 2 x - 1 và x + 3 = 4x + 4 tương đương
Ta có: 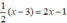 ⇔ x – 3 = 4x – 2 ⇔ x – 3 + 6 = 4x – 2 + 6 ⇔ x + 3 = 4x + 4.
⇔ x – 3 = 4x – 2 ⇔ x – 3 + 6 = 4x – 2 + 6 ⇔ x + 3 = 4x + 4.
Vậy hai phương trình 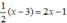 và x + 3 = 4x + 4 tương đương.
và x + 3 = 4x + 4 tương đương.
cho các phương trình sau đâu là 2 phương trình tương đương 3x+4=x-2; 2x=6; x=3; 3x=9
3x+4=x-2
=>3x-x=-2-4
=>2x=-6
=>x=-3
2x=6 nên x=3
3x=9 nên x=3
Vậy: Các phương trình 2x=6; x=3; 3x-9 là các phương trình tương đương
x2−5x+6=0x2−5x+6=0 (1)
x+(x−2)(2x+1)=2x+(x−2)(2x+1)=2 (2)
a. Chứng minh rằng hai phương trình có nghiệm chung là x = 2
b. Chứng minh rằng x = 3 là nghiệm của (1) nhưng không là nghiệm của (2)
c. Hai phương trình đã cho có tương đương với nhau không, vì sao ?
a. Thay x = 2 vào vế trái của phương trình (1), ta có:
22 – 5.2 + 6 = 4 – 10 + 6 = 0
Vế trái bằng vế phải nên x = 2 là nghiệm của phương trình (1).
Thay x = 2 vào vế trái của phương trình (2), ta có:
2 + (2 – 2)(2.2 +1) = 2 + 0 = 2
Vế trái bằng vế phải nên x = 2 là nghiệm của phương trình (2).
Vậy x = 2 là nghiệm chung của hai phương trình (1) và (2).
b. Thay x = 3 vào vế trái của phương trình (1), ta có:
32 – 5.3 + 6 = 9 – 15 + 6 = 0
Vế trái bằng vế phải nên x = 3 là nghiệm của phương trình (1).
Thay x = 3 vào vế trái của phương trình (2), ta có:
3 + (3 – 2)(2.3 + 1) = 3 + 7 = 10 ≠ 2
Vì vế trái khác vế phải nên x = 3 không phải là nghiệm của phương trình (2).
Vậy x = 3 là nghiệm của phương trình (1) nhưng không phải là nghiệm của phương trình (2).
c. Hai phương trình (1) và (2) không tương đương nhau vì x = 3 không phải là nghiệm chung của hai phương trình.
Xét sự tương đương của các phương trình sau ? 2x – 1 = 2 và (2x – 1)x = 2x
Ta có: (1) 2x – 1 = 2 ⇔ 2x = 3 ⇔ x = 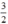
Phương trình 2x – 1 = 2 có tập nghiệm S = {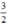 };
};
(2) (2x – 1)x = 2x ⇔ (2x – 1)x - 2x = 0 ⇔ x(2x - 1 – 2) = 0
⇔ x (2x - 3) = 0 ⇔ x = 0 hoặc 2x = 3 ⇔ x = 0 hoặc x = 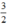
Phương trình (2x – 1)x = 2x có tập nghiệm S = { 0; 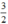 }
}
Vậy hai phương trình 2x – 1 = 2 và (2x – 1)x = 2x không tương đương vì không có cùng tập nghiệm