 cần gấppp ạ
cần gấppp ạ
GIÚP EM VỚI Ạ,CẢ 2 BÀI Ạ,EM CẦN GẤPPP
Bài 2:
a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: DM=DB
Ta có: CD=CM+MD
nên CD=CA+DB
giúp tớ với ạ, tớ cần gấppp
GIÚP EM VỚI Ạ,EM CẦN GẤPPP
GIÚP EM VỚI Ạ,EM CẦN GẤPPP
GIÚP EM VỚI Ạ,EM CẦN GẤPPP

Bài 2:
Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x+y=3\\3x-2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+2y=6\\3x-2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=1\end{matrix}\right.\)
Thay x=1 và y=1 vào (d), ta được:
\(2m-1+1=5m\)
\(\Leftrightarrow m=0\)
GIÚP EM VỚI Ạ,EM CẦN GẤPPP
Giúp tớ với ạ, tớ cần gấppp
a: góc BDC=180-60=120 độ
góc BOC=2*góc BAC=120 độ
góc BAD=góc CAD=60/2=30 độ
=>góc BOD=góc COD=60 độ
góc BOD=1/2*góc BOC
=>OD là phân giác của góc BOC
Xét ΔOBD có OB=OD và góc BOD=60 độ
nên ΔOBD đều
=>góc OBD=60 độ
Xét ΔOCD có OD=OC và góc DOC=60 độ
=>ΔOCD đều
=>góc OCD=60 độ
Xét tứ giác BOCD có
góc BOC=góc BDC
góc OBD=góc OCD
OB=OC
=>BOCD là hình thoi
b:
góc IBC+góc ICB=1/2(góc ABC+góc ACB)=1/2*120=60 độ
=>góc BIC=120 độ
góc BOC=góc BIC=120 độ
=>BOIC nội tiếp
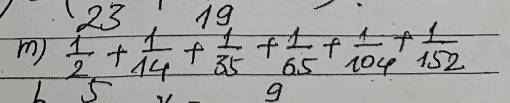
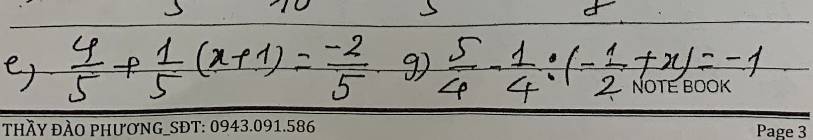
cần giúp 3 phần này ạ gấppp
m: \(\dfrac{1}{2}+\dfrac{1}{14}+\dfrac{1}{35}+\dfrac{1}{65}+\dfrac{1}{104}+\dfrac{1}{152}\)
\(=\dfrac{2}{4}+\dfrac{2}{28}+\dfrac{2}{70}+\dfrac{2}{130}+\dfrac{2}{208}+\dfrac{2}{304}\)
\(=\dfrac{2}{1\cdot4}+\dfrac{2}{4\cdot7}+\dfrac{2}{7\cdot10}+\dfrac{2}{10\cdot13}+\dfrac{2}{13\cdot16}+\dfrac{2}{16\cdot19}\)
\(=\dfrac{2}{3}\left(\dfrac{3}{1\cdot4}+\dfrac{3}{4\cdot7}+\dfrac{3}{7\cdot10}+\dfrac{3}{10\cdot13}+\dfrac{3}{13\cdot16}+\dfrac{3}{16\cdot19}\right)\)
\(=\dfrac{2}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{16}-\dfrac{1}{19}\right)\)
\(=\dfrac{2}{3}\cdot\dfrac{18}{19}=\dfrac{12}{19}\)
e: \(\dfrac{4}{5}+\dfrac{1}{5}\left(x+1\right)=-\dfrac{2}{5}\)
=>\(\dfrac{1}{5}\left(x+1\right)=-\dfrac{2}{5}-\dfrac{4}{5}=-\dfrac{6}{5}\)
=>x+1=-6
=>x=-6-1=-7
g: \(\dfrac{5}{4}-\dfrac{1}{4}:\left(-\dfrac{1}{2}+x\right)=-1\)
=>\(\dfrac{1}{4}:\left(x-\dfrac{1}{2}\right)=\dfrac{5}{4}+1=\dfrac{9}{4}\)
=>\(x-\dfrac{1}{2}=\dfrac{1}{4}:\dfrac{9}{4}=\dfrac{1}{9}\)
=>\(x=\dfrac{1}{9}+\dfrac{1}{2}=\dfrac{11}{18}\)
GIÚP EM BÀI NÀY VỚI Ạ,EM CẦN GẤPPP
\(a,\Leftrightarrow\left\{{}\begin{matrix}8x+12y=16\\8x+12y=-3\end{matrix}\right.\Leftrightarrow HPT.vô.nghiệm\\ b,\Leftrightarrow\left\{{}\begin{matrix}2x-2y+6x+3y=5\\5x+5y-4x+2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8x+y=5\\x+7y=2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}56x+7y=35\\x+7y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=\dfrac{1}{5}\end{matrix}\right.\\ c,\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{6}+\dfrac{y}{8}=\dfrac{5}{2}\\\dfrac{x}{6}+\dfrac{y}{9}=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{2}+\left(-\dfrac{11}{18}\right)=2\\y=\dfrac{2}{3}-\dfrac{5}{2}=-\dfrac{11}{6}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{47}{9}\\y=-\dfrac{11}{6}\end{matrix}\right.\)
\(d,ĐK:x\ne-2;y\ne1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x+2}-\dfrac{6}{y-1}=4\\\dfrac{2}{x+2}+\dfrac{2}{y-1}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+2}-\dfrac{3}{y-1}=2\\\dfrac{8}{y-1}=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+2}=2+\dfrac{3}{8}=\dfrac{19}{8}\\y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{30}{19}\\y=9\end{matrix}\right.\)
\(e,\Leftrightarrow\left\{{}\begin{matrix}x^2=4-y^2\\3\left(4-y^2\right)-2y^2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2=4-y^2\\12-5y^2=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x^2=4-y^2\\y^2=\dfrac{9}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2=\dfrac{11}{5}\\y^2=\dfrac{9}{5}\end{matrix}\right.\)
Vậy hpt có nghiệm \(\left(x;y\right)=\left\{\left(\pm\dfrac{\sqrt{55}}{5};\pm\dfrac{3\sqrt{5}}{5}\right)\right\}\)