 Giải giúp mik câu 1, với camon
Giải giúp mik câu 1, với camon
H24
Những câu hỏi liên quan

Mn giúp mik câu 3 với 8 ạ, camon nhiu:3333
1) Ta có: \(P=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-1\right)\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-1}{1}\)
\(=\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}\)
2) Thay \(x=4-2\sqrt{3}\) vào P, ta được:
\(P=\dfrac{2\left(\sqrt{3}-1\right)+1}{\sqrt{3}-1+1}=\dfrac{2\sqrt{3}-2+1}{\sqrt{3}}=\dfrac{2\sqrt{3}-1}{\sqrt{3}}=\dfrac{6-\sqrt{3}}{3}\)
Đúng 1
Bình luận (2)
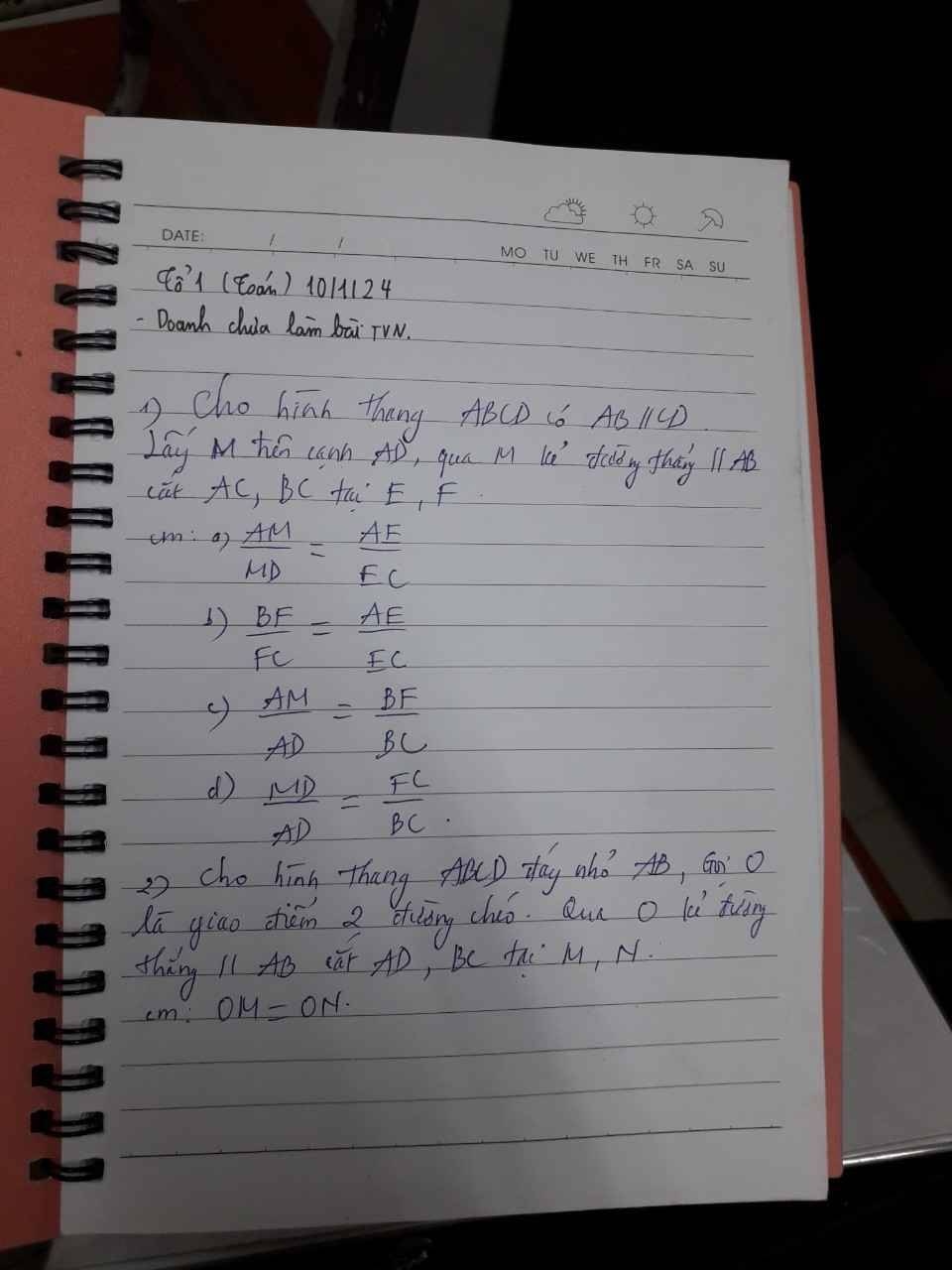
Câu 1:
a: Xét ΔADC có ME//DC
nên \(\dfrac{AM}{MD}=\dfrac{AE}{EC}\)
b: Xét ΔCAB có EF//AB
nên \(\dfrac{CE}{EA}=\dfrac{CF}{FB}\)
=>\(\dfrac{AE}{EC}=\dfrac{BF}{FC}\)
c: ta có: \(\dfrac{AM}{MD}=\dfrac{AE}{EC}\)
\(\dfrac{AE}{EC}=\dfrac{BF}{FC}\)
Do đó: \(\dfrac{AM}{MD}=\dfrac{BF}{FC}\)
d: Ta có: \(\dfrac{AM}{MD}=\dfrac{BF}{FC}\)
=>\(\dfrac{AM+MD}{MD}=\dfrac{BF+FC}{FC}\)
=>\(\dfrac{AD}{MD}=\dfrac{BC}{FC}\)
=>\(\dfrac{DM}{DA}=\dfrac{CF}{CB}\)
Bài 2:
Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AM}{AD}\)(1)
Xét ΔBDC có ON//DC
nên \(\dfrac{ON}{DC}=\dfrac{BN}{BC}\left(2\right)\)
Xét hình thang ABCD có MN//AB//CD
nên \(\dfrac{AM}{MD}=\dfrac{BN}{NC}\)
=>\(\dfrac{MD}{AM}=\dfrac{CN}{BN}\)
=>\(\dfrac{MD+AM}{AM}=\dfrac{CN+BN}{BN}\)
=>\(\dfrac{AD}{AM}=\dfrac{BC}{BN}\)
=>\(\dfrac{AM}{AD}=\dfrac{BN}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra OM=ON
Đúng 2
Bình luận (1)
Giúp mik mấy câu này vs ạ=((. Mik camon nhìuuu


Giúp mik mấy câu này vs ạ=((. Mik camon nhìuuu

Mn giúp mik câu i,k,m ạ. Mik camon nhìuu
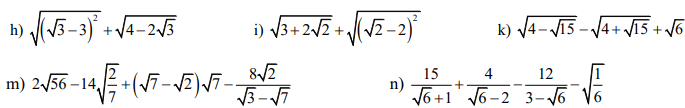
i) \(\sqrt{3+2\sqrt{2}}+\sqrt{\left(\sqrt{2}-2\right)^2}=\sqrt{\left(\sqrt{2}\right)^2+2.\sqrt{2}.1+1^2}+\left|\sqrt{2}-2\right|\)
\(=\sqrt{\left(\sqrt{2}+1\right)^2}+2-\sqrt{2}=\left|\sqrt{2}+1\right|+2-\sqrt{2}=\sqrt{2}+1+2-\sqrt{2}=3\)
k) \(\sqrt{4-\sqrt{15}}-\sqrt{4+\sqrt{15}}+\sqrt{6}=\sqrt{\dfrac{8-2\sqrt{15}}{2}}-\sqrt{\dfrac{8+2\sqrt{15}}{2}}+\sqrt{6}\)
\(=\sqrt{\dfrac{\left(\sqrt{5}\right)^2-2.\sqrt{5}.\sqrt{3}+\left(\sqrt{3}\right)^2}{2}}-\sqrt{\dfrac{\left(\sqrt{5}\right)^2+2.\sqrt{5}.\sqrt{3}+\left(\sqrt{3}\right)^2}{2}}+\sqrt{6}\)
\(=\sqrt{\dfrac{\left(\sqrt{5}-\sqrt{3}\right)^2}{2}}-\sqrt{\dfrac{\left(\sqrt{5}+\sqrt{3}\right)^2}{2}}+\sqrt{6}\)
\(=\dfrac{\left|\sqrt{5}-\sqrt{3}\right|}{\sqrt{2}}-\dfrac{\left|\sqrt{5}+\sqrt{3}\right|}{\sqrt{2}}+\sqrt{6}\)
\(=\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}-\dfrac{\sqrt{5}+\sqrt{3}}{\sqrt{2}}+\sqrt{6}=\dfrac{-2\sqrt{3}}{\sqrt{2}}+\sqrt{6}=-\sqrt{6}+\sqrt{6}=0\)
m) \(2\sqrt{56}-14\sqrt{\dfrac{2}{7}}+\left(\sqrt{7}-\sqrt{2}\right)\sqrt{7}-\dfrac{8\sqrt{2}}{\sqrt{3}-\sqrt{7}}\)
\(=2\sqrt{4.14}-2\sqrt{49.\dfrac{2}{7}}+7-\sqrt{14}+\dfrac{8\sqrt{2}.\left(\sqrt{7}+\sqrt{3}\right)}{\left(\sqrt{7}-\sqrt{3}\right)\left(\sqrt{7}+\sqrt{3}\right)}\)
\(=4\sqrt{14}-2\sqrt{14}+7-\sqrt{14}+\dfrac{8.\left(\sqrt{14}+\sqrt{6}\right)}{4}\)
\(=\sqrt{14}+7+2\left(\sqrt{14}+\sqrt{6}\right)=7+3\sqrt{14}+2\sqrt{6}\)
Đúng 1
Bình luận (0)
Lời giải:
i.
\(=\sqrt{(\sqrt{2}+1)^2}+|\sqrt{2}-2|=|\sqrt{2}+1|+|\sqrt{2}-2|=\sqrt{2}+1+2-\sqrt{2}=3\)
k.
\(=\frac{1}{\sqrt{2}}(\sqrt{8-2\sqrt{15}}-\sqrt{8+2\sqrt{15}}+\sqrt{12})\)
\(=\frac{1}{\sqrt{2}}(\sqrt{(\sqrt{3}-\sqrt{5})^2}-\sqrt{(\sqrt{3}+\sqrt{5})^2}+2\sqrt{3})\)
\(=\frac{1}{\sqrt{2}}(|\sqrt{3}-\sqrt{5}|-|\sqrt{3}+\sqrt{5}|+2\sqrt{3})=\frac{1}{\sqrt{2}}(-2\sqrt{3}+2\sqrt{3})=0\)
m.
\(=4\sqrt{14}-2\sqrt{14}+7-\sqrt{14}-\frac{8\sqrt{2}(\sqrt{3}+\sqrt{7})}{(\sqrt{3}-\sqrt{7})(\sqrt{3}+\sqrt{7})}\)
\(=\sqrt{14}+7-\frac{8(\sqrt{14}+\sqrt{6})}{-4}=\sqrt{14}+\sqrt{7}+2(\sqrt{14}+\sqrt{6})=3\sqrt{14}+\sqrt{7}+2\sqrt{6}\)
Đúng 0
Bình luận (0)
Giúp mik câu 2 vs ạ. Camon ạ
Bài 1:
a) Xét ΔMNQ và ΔENQ có
NM=NE(gt)
\(\widehat{MNQ}=\widehat{ENQ}\)
NQ chung
Do đó: ΔMNQ=ΔENQ(c-g-c)
Suy ra: QM=QE(hai cạnh tương ứng)
Đúng 1
Bình luận (0)
Bài 1:
b) Ta có: ΔQMN=ΔQEN(cmt)
nên \(\widehat{QMN}=\widehat{QEN}\)(hai góc tương ứng)
mà \(\widehat{QMN}=90^0\)(gt)
nên \(\widehat{QEN}=90^0\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
S3= 1+4+7+...+82 ( giúp mik với ạ,mik tính bị dư . Mik camon trc )
S = 1 + 4 + 7 + .....+ 82
dãy số trên là dãy số cách đều với khoảng cách là: 4 - 1 = 3
Số số hạng của dãy số trên là : ( 82 - 1) : 3 + 1 = 28
Tổng S = ( 82+1).28 : 2 = 1162
Đúng 2
Bình luận (0)

GIẢI GIÚP MIK BÀI 1,2 GỒM TÓM TẮT ĐẦY ĐỦ MIK CAMON GẤC NHÌU NHÌU Ạ
\(1.\Rightarrow\left\{{}\begin{matrix}a,L=\dfrac{RS}{p}=\dfrac{10.0,1.10^{-6}}{0,4.10^{-5}}=0,25m\\b,\Rightarrow L=\dfrac{RS}{p}=\dfrac{30.0,5.10^{-6}}{1,7.10^{-8}}=882m\\c,\Rightarrow S=\dfrac{pL}{R}=\dfrac{0,5.10^{-6}.100}{50}=10^{-6}m^2\\\end{matrix}\right.\)
\(2.\Rightarrow Vàng,Nhôm,ĐỒng,Sắt\)
thông thường Đồng được sử dụng nhiều nhất do vật liệu không quá đắt
so với Vàng,Nhôm
Đúng 1
Bình luận (1)

mn ơi giúp mik giải mấy bài đó đc hog :< mik bí quá à :< camon mn trc vì đã help mik :3
1:
#include <bits/stdc++.h>
using namespace std;
long long t,i,n;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++) t+=i;
cout<<t;
return 0;
}
Bài 2:
#include <bits/stdc++.h>
using namespace std;
long long n,i,t;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++)
if (i%2==0) t+=i;
cout<<t;
return 0;
}
Đúng 2
Bình luận (1)
Bài 3:
#include <bits/stdc++.h>
using namespace std;
long long n,i,t;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++)
if (i%2!=0) t+=i;
cout<<t;
return 0;
}
Bài 4:
#include <bits/stdc++.h>
using namespace std;
long long n,i,t;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++)
if (i%3==0) t+=i;
cout<<t;
return 0;
}
Bài 5:
#include <bits/stdc++.h>
using namespace std;
long long n,i,t;
int main()
{
cin>>n;
t=1;
for (i=1; i<=n; i++)
t*=i;
cout<<t;
return 0;
}
Đúng 1
Bình luận (0)




