tìm 2 số tự nhiên a,b thỏa mãn a-b=a/b
LI
Những câu hỏi liên quan
a) Tìm số tự nhiên a,b thỏa mãn 10 mũ a+483=b mũ 2
b) Tìm các số tự nhiên a, b,c thỏa mãn: a mũ 2+ab+ác=20×ab+b mũ 2+BC=180×ac+BC+c mũ 2=200
a) \(10^a+483=b^2\) (*)
Nếu \(a=0\) thì (*) \(\Leftrightarrow b^2=484\Leftrightarrow b=22\)
Nếu \(a\ge1\) thì VT (*) chia 10 dư 3, mà \(VP=b^2\) không thể chia 10 dư 3 nên ta có mâu thuẫn. Vậy \(\left(a,b\right)=\left(0,22\right)\) là cặp số tự nhiên duy nhất thỏa mãn điều kiện bài toán.
(Chú ý: Trong lời giải đã sử dụng tính chất sau của số chính phương: Các số chính phương khi chia cho 10 thì không thể dư 2, 3, 7, 8. Nói cách khác, một số chính phương không thể có chữ số tận cùng là 2, 3, 7, 8)
b) Bạn gõ lại đề bài nhé, chứ mình nhìn không ra :))
Đúng 0
Bình luận (0)
tìm 2 số tự nhiên a và b thỏa mãn (a+b).(a-b) =2014
tìm 2 số tự nhiên a và b thỏa mãn:(a,b)+[a,b]=55
Gọi(a;b)=d, a=dm, b=dn, (m,n)=1,d,m,n thuộc N*
Ta có:a.b=(a,b).[a.b]
=>[a.b]=a.b:(a.b)
Theo đề bài ta có:
[a,b]+(a,)=55
=>a.b:(a,b)+(a,b)=55
Thay vào ta có:
dm.dn:d+d=55
=>d.mn+d=55
=>d.(mn+1)=55
Vì d,m,n thuộc N*, Gỉa sử a>b thì m>n ta có bảng sâu:
| d | mn+1 | m | n | a | b |
| 1 | 55 | 54 | 1 | 54 | 1 |
| 5 | 11 | 10 5 | 1 2 | 50 25 | 5 10 |
| 11 | 5 | 4 | 1 | 44 | 11 |
Vậy(a,b)thuộc{(54,1);(50,5);(25,10);(44,11)}
Đúng 0
Bình luận (0)
Tìm cặp số tự nhiên a và b thỏa mãn a/2+b/3=a+b/5
Tìm số tự nhiên để 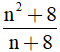 là số tự nhiên.
là số tự nhiên.
Cho các số a, b thỏa mãn a + b = 2 và a.b = - 2. Tính a7 + b7.
a: Để A là số tự nhiên thì \(n+8\in\left\{8;9;12;18;24;36;72\right\}\)
hay \(n\in\left\{0;1;3;10;18;28;64\right\}\)
Đúng 0
Bình luận (0)
số tự nhiên ab thỏa mãn a,b : (a+b)=0,5.Tìm cặp số tự nhiên ab.
Từ đề bài suy ra:\(\frac{a,b}{a+b}=\frac{1}{2}\)
\(\Rightarrow a,b.2=a+b\)
\(\Rightarrow2a+0,b.2=a+b\)
\(\Rightarrow2a-a=b-0,2.b\)
\(\Rightarrow a=b\left(1-0,2\right)\)
\(\Rightarrow a=\frac{4}{5}b\)
\(\Rightarrow\frac{a}{b}=\frac{4}{5}\)
\(\Rightarrow a=4,b=5\)
Đúng 0
Bình luận (0)
a) Tìm số tự nhiên n biết (4n+2) ⋮ (n+1)
b) Tìm các số nguyên a và b thỏa mãn: (a+2).(b-1)=9
Cíuuu tuiiii
a: =>4n+4-2 chia hết cho n+1
=>\(n+1\in\left\{1;-1;2;-2\right\}\)
mà n là số tự nhiên
nên \(n\in\left\{0;1\right\}\)
b: \(\Leftrightarrow\left(a+2;b-1\right)\in\left\{\left(1;9\right);\left(9;1\right);\left(-1;-9\right);\left(-9;-1\right);\left(3;3\right);\left(-3;-3\right)\right\}\)
=>\(\left(a,b\right)\in\left\{\left(-1;10\right);\left(7;2\right);\left(-3;-8\right);\left(-11;0\right);\left(1;4\right);\left(-5;-2\right)\right\}\)
Đúng 0
Bình luận (0)
Cho 2 số tự nhiên a; b thỏa mãn ƯCLN(a, b) = 1. Tìm ƯCLN( a2, b)
Cho 2 số tự nhiên a; b thỏa mãn ƯCLN(a, b) = 1. Tìm ƯCLN( a2, b)


