Giúp mình với câu D, e, f bài 1 với bài 2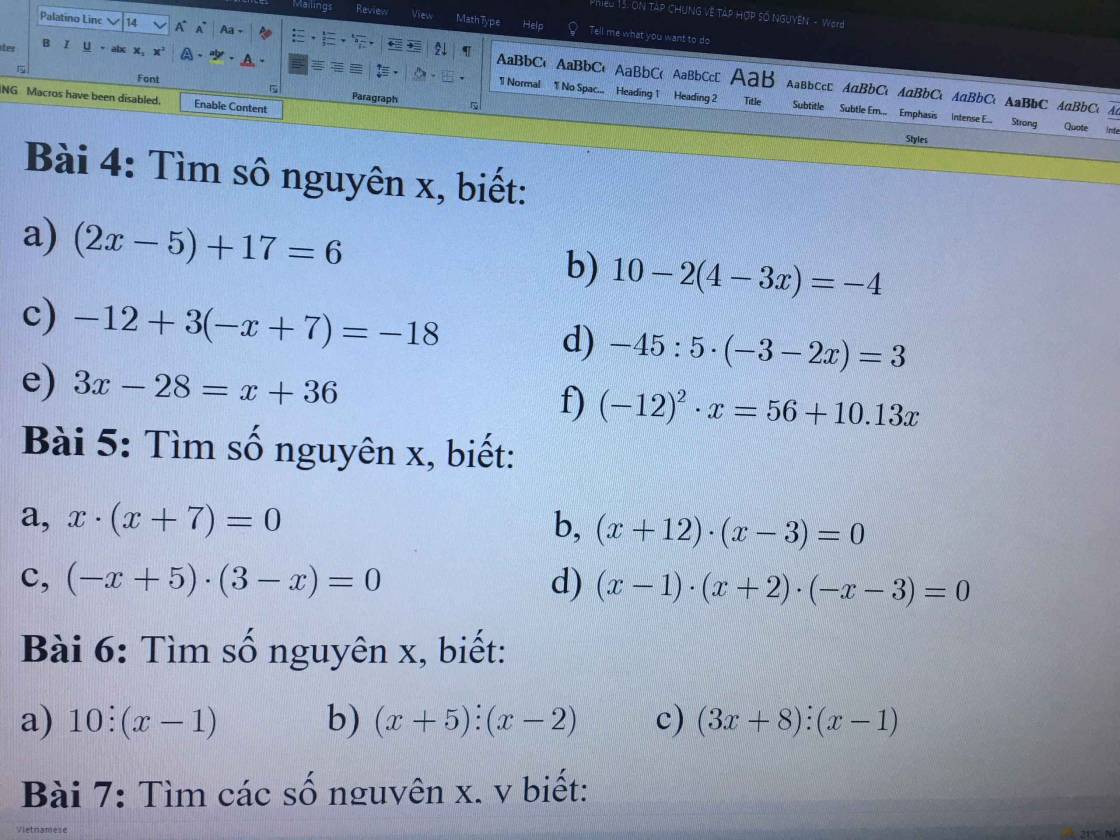
TA
Những câu hỏi liên quan
Moị người giúp em bài 1 câu d,e,f với ạ
Bài 3 câu b và câu d
Bài 4 câu c và d
Bài 5 câu d,e,f giải
giúp mình với ạ cần gấp trong tối nay cả 3 bài

cái gì vậy bạn
? bài ở đâu
ko đăng ảnh đc ạ
Xem thêm câu trả lời
Giúp em giải
bài 1 tìm nghiệm các hàm số: p, o, l, q
bài 2 câu e, f với ạ
em cám ơn ạ 

j, ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
\(tan\left(\dfrac{\pi}{3}+x\right)-tan\left(\dfrac{\pi}{6}+2x\right)=0\)
\(\Leftrightarrow tan\left(\dfrac{\pi}{3}+x\right)=tan\left(\dfrac{\pi}{6}+2x\right)\)
\(\Leftrightarrow\dfrac{\pi}{3}+x=\dfrac{\pi}{6}+2x+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\left(l\right)\)
\(\Rightarrow\) vô nghiệm.
Đúng 1
Bình luận (0)
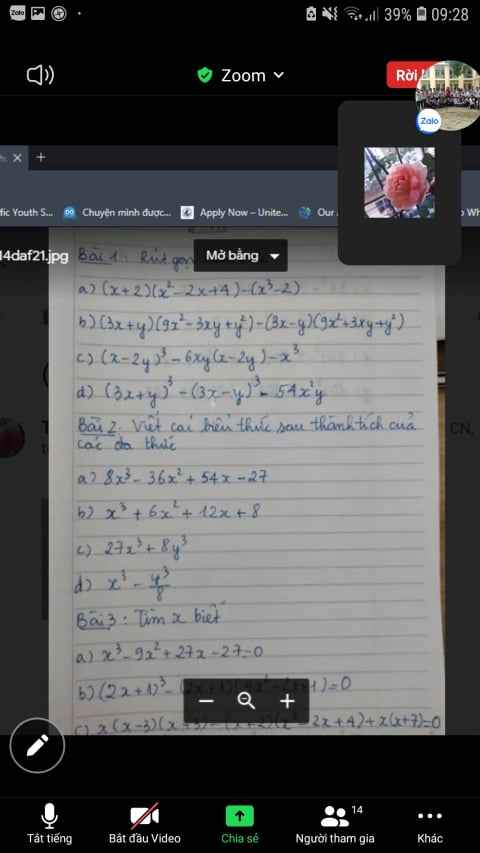
làm giúp mình bài 2 với câu d bài 1 vs ạ
Em hãy đăng bài ở môn Toán nhé!
Đúng 2
Bình luận (1)
Bài 2:
a: \(8x^3-36x^2+54x-27=\left(2x-3\right)^3\)
b: \(x^3+6x^2+12x+8=\left(x+2\right)^3\)
c: \(27x^3+8y^3=\left(3x+2y\right)\left(9x^2-6xy+4y^2\right)\)
d: \(x^3-\dfrac{y^3}{8}=\left(x-\dfrac{1}{2}y\right)\left(x^2+\dfrac{1}{2}xy+\dfrac{1}{4}y^2\right)\)
Đúng 2
Bình luận (0)
mọi ng giải giúp em câu e,f bài 1 với ạ
e:
\(E=\left(\dfrac{\sqrt{15}-\sqrt{20}}{2-\sqrt{3}}+\dfrac{\sqrt{21}-\sqrt{7}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(-\dfrac{\sqrt{5}\left(2-\sqrt{3}\right)}{2-\sqrt{3}}-\dfrac{\sqrt{7}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}\right)\cdot\dfrac{\sqrt{7}-\sqrt{5}}{1}\)
\(=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
=-2
f: \(F=\sqrt{3}+1+2-\sqrt{3}=3\)
Đúng 2
Bình luận (0)
Vẽ hệ trục tọa độ Oxy và đánh dấu các điểm:
A(2;-2), B(-1;1), C(4;0), D(3;3), E(2,2), F(-1;4)
mn giúp mình giải bài này với ạ mình cảm ơn .
GIÚP EM CÂU C,D,E BÀI 1.BÀI 2,3 VỚI Ạ.EM CẦN GẤPP
GIÚP EM BÀI GIẢI PT VÀ CÂU C,D,E BÀI 2 VỚI Ạ..
\(b,B=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}-8}{x-5\sqrt{x}+6}\left(x\ge0;x\ne4;x\ne9\right)\\ B=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-4+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)
\(c,B< A\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}< \dfrac{\sqrt{x}+1}{\sqrt{x}-2}\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}< 0\\ \Leftrightarrow\dfrac{-5}{\sqrt{x}-2}< 0\Leftrightarrow\sqrt{x}-2>0\left(-5< 0\right)\\ \Leftrightarrow x>4\\ d,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=\dfrac{\sqrt{x}-4}{\sqrt{x}+1}=1-\dfrac{5}{\sqrt{x}+1}\in Z\\ \Leftrightarrow5⋮\sqrt{x}+1\Leftrightarrow\sqrt{x}+1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{-6;-2;0;4\right\}\\ \Leftrightarrow x\in\left\{0;16\right\}\left(\sqrt{x}\ge0\right)\)
\(e,P=1-\dfrac{5}{\sqrt{x}+1}\)
Ta có \(\sqrt{x}+1\ge1,\forall x\Leftrightarrow\dfrac{5}{\sqrt{x}+1}\ge5\Leftrightarrow1-\dfrac{5}{\sqrt{x}+1}\le-4\)
\(P_{max}=-4\Leftrightarrow x=0\)
Đúng 2
Bình luận (0)
Vẽ hệ trục tọa độ Oxy và đánh dấu các điểm:
A(2;-2), B(-1;1), C(4;0), D(3;3), E(2,2), F(-1;4)
mọi người giúp mình giải bài này với ạ mình cảm ơn nhìu




