Tìm số tự nhiên a; b biết
a) 7/5 < y/40 < 8/5
b) 50/19 x 38/25 < y < 69/17 + 33/17
1. Tìm số tự nhiên A để phân số 15/a-2 là số tự nhiên.
2.Tìm số tự nhiên A để phân số a+8/a+1 là số tự nhiên.
3.Tìm số tự nhiên A để phân số 2.a+11/a+1 là số tự nhiên.
4. Chứng tỏ :1<a/b+c+b/c+a+c/a+b<2
a bằng giá trị trung bình cộng của 7,11 và a. Vì vậy a có giá trị bằng trung bình cộng của 7 và 11.
Số tự nhiên a cần tìm là:
(7+11):2=9
Đáp số: a là 9
Cho ba số tự nhiên 7,11 và a. Biết số tự nhiên a bằng trung bình cộng của 3 số tự nhiên đã cho. Tìm số tự nhiên a.
Giải toán bằng sơ đồ đoạn thẳng của tiểu học em nhé
Tổng của hai số 7 và 11 là: 7 + 11 = 18
Coi trung bình cộng của ba số là 1 phần ta có sơ đồ
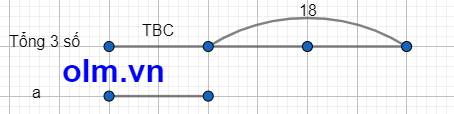
theo sơ đồ ta có:
Số tự nhiên a là: 18 : 2 = 9
Đáp số: 9
A, Tìm số tự nhiên lớn nhất có 3 chữ số
B, Tìm số tự nhiên lớn nhất có 3 chữ số khác nhau
C,Tìm số tự nhiên chẵn nhỏ nhất có 5 chữ số
D, Tìm số tự nhiên chẵn lớn nhất có 5 chữ số khác nhau
1) Hãy cho biết số tự nhiên 12 bằng tích của hai số nào?
2) Tích của hai số tự nhiên a và b bằng 12 . Tìm a và b, biết a < b .
3) Hãy cho biết số tự nhiên 30 bằng tích của hai số tự nhiên nào?
4) Tích của hai số tự nhiên a và b bằng 30 . Tìm a và b, a > b .
1) 12 = 1.12 = 2.6 = 3.4 = 4.3 = 6.2 = 12.1
2) 12 = 1.12 = 2.6 = 3.4
Vậy (a; b) ∈ {(1; 12); (2; 6); (3; 4)}
3) 30 = 1.30 = 2.15 = 3.10 = 5.6 = 6.5 = 10.3 = 15.2 = 30.1
4) 30 = 30.1 = 15.2 = 10.3 = 6.5
Vậy (a; b) ∈ {(30; ); (15; 2); (10; 3); (6; 5)}
a, Ta có: 12 = 1 x 12; 2 x 6; 3 x 4
b, Ta có: 12 = 1 x 12; 2 x 6; 3x 4
Theo đề bài, ta có điều kiện: a < b
=> a ϵ {1; 2; 3}
=> b ϵ {12; 6; 4}
Vậy các cặp số (a; b) cần tìm là:
(a; b) ϵ {(1; 12); (2; 6); (3; 4)}
c, Ta có: 30 = 1 x 30; 2 x 15; 3 x 10; 5 x 6
d, Ta có: 30 = 1 x 30; 2 x 15; 3 x 10; 5 x 6
Theo đề bài, ta có điều kiện: a > b
=> a = 30; b = 1
=> a = 15; b = 2
=> a = 10; b = 3
=> a = 6; b = 5
Vậy ta có các cặp số (a; b) thỏa mãn đề bài là:
(a; b) ϵ {(30; 1); (15; 2); (10; 3); (6; 5}
a. tìm a là số tự nhiên để 17a+8 là số chính phương
b. tìm a là số tự nhiên để 13a+a là số chính phương
c. tìm n là số tự nhiên sao cho 3n+4 là số chính phương
d. tìm n là số tự nhiên sao cho 2n+9 là số chính phương
a. tìm a là số tự nhiên để 17a+8 là số chính phương
Giả sử \(17a+8=x^2\Rightarrow17a-17+25=x^2\Rightarrow17\left(a-1\right)=x^2-25\Rightarrow17\left(a-1\right)=\left(x-5\right)\left(x+5\right)\)
\(\Rightarrow\left(x-5\right);\left(x+5\right)⋮17\)
\(\Rightarrow x=17n\pm5\Rightarrow a=17n^2\pm10n+1\)
Tìm số tự nhiên a nhỏ nhất sao cho khi chia a cho 3/5 và chia a cho 10/7 ta đều dc kết quả là số tự nhiên. Tìm số tự nhiên a
a chia 3/5 thuộc N=)3a chia hết cho 5=)30a chia hết cho 50
a chia 10/7 thuộc N=)10a chia hết cho 7=)30a chia hết cho 21
=)30a chia hết cho BCNN(50,21)
=)30a chia hết cho 1050
=)a chia hết cho 350
mà a nhỏ nhất =)a=350
a) Tìm số tự nhiên a lớn nhất sao cho : 3,5 x a < 12 : ………………………………
b) Tìm số tự nhiên b bé nhất sao cho : 8,7 x b > 64 : …………………………………
c) Tìm số tự nhiên x biết : 10,67 < x x 2 < 12,35 : ………………………………
d) Tìm số ab biết : 1,01 x ab = 2b,a3 : ……………………………
\(a=0;1;2;3\) ở câu a
\(a=0;1;2;3;4;5;6;7\) ở câu b
\(a=0;1;2;3;4;5;6\) ở câu c
a) a = 3
b) b = 8
c) x = 1
d) ab = 23
a. Tìm số tự nhiên nhỏ nhất khác 5 khi chia số đó cho 70 , 140 , 350 , 700 đều dư 5
b. Tìm số tự nhiên nhỏ nhất khi chia cho 3 dư 1 chia cho 5 dư 3 và chia cho 7 dư 5
c. Tìm số tự nhiên nhỏ nhất khi chia cho 5 dư 1 , chia cho 7 dư 5
d. Tìm số tự nhiên a nhỏ nhất, biết rằng a chia cho 5,7,9 thì số dư lần lượt là 3,4,5
b.Gọi số cần tìm là a.
Ta có: a : 3 dư 1 \(\Rightarrow\) a + 2 \(⋮\) 3
a : 5 dư 3 \(\Rightarrow\) a + 2 \(⋮\) 5 và a là nhỏ nhất
a : 7 dư 5 \(\Rightarrow\) a + 2 \(⋮\) 7
\(\Rightarrow\) a + 2 \(\in\) BCNN( 3, 5, 7 ).
\(\Rightarrow\) BCNN( 3, 5, 7 ) = 3.5.7 = 105.
\(\Rightarrow\) a + 2 = 105
\(\Rightarrow\) a = 103
câu 1: tìm số tự nhiên x, biết : 38,46 <x< 39,08 số tự nhiên đó là: help
câu 2: tìm chữ số a, biết: 86,718 > 86,7a9 số tự nhiên đó là: help
Câu 1:
38,46 < 39 < 39,08
Vậy x = 39
Câu 2:
86,718 > 86,709
Vậy a = 0