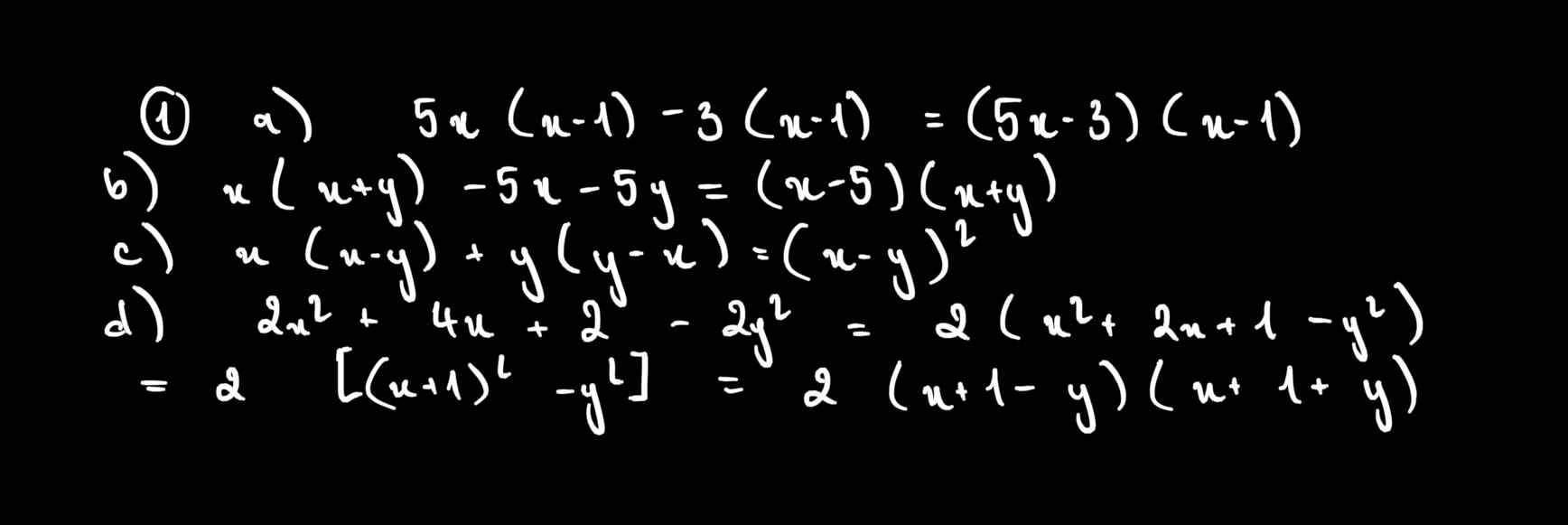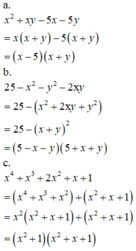Phân tích đa thức thành nhân tử 2x2 + 5x - 3
DQ
Những câu hỏi liên quan
Phân tích đa thức thành nhân tử:
2x2+5x+3
\(2x^2+5x+3=2x^2+2x+3x+3=2x\left(x+1\right)+3\left(x+1\right)=\left(2x+3\right)\left(x+1\right)\)
Đúng 0
Bình luận (0)
\(2x^2+5x+3=2x^2+2x+3x+3=\left(2x^2+2x\right)+\left(3x+3\right)=2x\left(x+1\right)+3\left(x+1\right)=\left(x+1\right)\left(2x+3\right)\)
Đúng 2
Bình luận (0)
Chứng tỏ rằng nếu phương trình ax2 + bx + c = 0 có nghiệm là x1 và x2 thì tam thức ax2 + bx + c phân tích được thành nhân tử như sau:
ax2 + bx + c = a( x - x1)(x - x2)
Áp dụng : phân tích đa thức thành nhân tử.
2x2 - 5x + 3
* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: 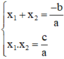
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 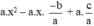
= a.x2 + bx + c (đpcm).
* Áp dụng:
a) 2x2 – 5x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 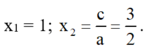
Vậy: 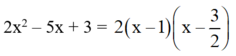
Đúng 0
Bình luận (0)
Chứng tỏ rằng nếu phương trình
a
x
2
+
b
x
+
c
0
có nghiệm là
x
1
v
à
x
2
thì tam thức
a
x
2
+
b
x
+...
Đọc tiếp
Chứng tỏ rằng nếu phương trình a x 2 + b x + c = 0 có nghiệm là x 1 v à x 2 thì tam thức a x 2 + b x + c phân tích được thành nhân tử như sau:
a x 2 + b x + c = a ( x - x 1 ) ( x - x 2 )
Áp dụng : phân tích đa thức thành nhân tử.
a ) 2 x 2 - 5 x + 3 ; b ) 3 x 2 + 8 x + 2
* Chứng minh:
Phương trình a x 2 + b x + c = 0 có hai nghiệm x 1 ; x 2
⇒ Theo định lý Vi-et: 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
= a . x 2 + b x + c ( đ p c m ) .
* Áp dụng:
a) 2 x 2 – 5 x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 
Vậy: 
b) 3 x 2 + 8 x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ ’ = 4 2 – 2 . 3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:

Đúng 0
Bình luận (0)
Phân tích đa thức 2x2 - 7 + 3 thành nhân tử.
\(2x^2-7+3=2x^2-6x-x+3=2x\left(x-3\right)-\left(x-3\right)=\left(x-3\right)\left(2x-1\right)\)
Đúng 0
Bình luận (0)
\(2x^2-7+3\\ =2x^2-4\\ =2\left(x^2+2\right).\)
Đúng 0
Bình luận (1)
\(2x^2-7+3\\ =2x^2-\left(7-3\right)\\ =2x^2-4\\ =2\left(x^2-2\right)\)
Đúng 1
Bình luận (0)
phân tích đa thức thành nhân tử :
a) x2 - 6x +5
b) x2 - x - 12
c) x2 + 8x +15
d) 2x2 - 5x -12
e) x2 - 13x + 36
a: \(x^2-6x+5=\left(x-5\right)\left(x-1\right)\)
b: \(x^2-x-12=\left(x-4\right)\left(x+3\right)\)
c: \(x^2+8x+15=\left(x+5\right)\left(x+3\right)\)
d: \(2x^2-5x-12=\left(x-4\right)\left(2x+3\right)\)
e: \(x^2-13x+36=\left(x-9\right)\left(x-4\right)\)
Đúng 0
Bình luận (0)
Bài 1: Phân tích các đa thức sau thành nhân tử:
a) 5x(x – 1) – 3(x – 1) b)x(x + y) – 5x – 5y
c) x(x – y) + y(y – x) d) 2x2 + 4x + 2 – 2y2
a) = (x - 1)(5x - 3)
b) = x(x + y) - 5(x + y)
= (x + y)(x - 5)
c) = x(x - y) - y(x - y)
= (x - y)^2
d) = 2(x2 + 2x + 1 - y2)
= 2[(x + 1)2 - y2]
= 2(x - y + 1)(x + y + 1)
Đúng 1
Bình luận (0)
Phân tích các đa thức sau thành nhân tửa)
x
2
+
x
y
−
5
x
−
5
y
b)
25
−
x
2
−
y
2
−
2
x
y
c)
x
4
+
x
3
+
2
x
2
+...
Đọc tiếp
Phân tích các đa thức sau thành nhân tử
a) x 2 + x y − 5 x − 5 y
b) 25 − x 2 − y 2 − 2 x y
c) x 4 + x 3 + 2 x 2 + x + 1
Phân tích đa thức thành nhân tử
a/ 3x3y2-12x2y3
b/x2-5x+xy-5y
c/x4+64y
d/2x2-4xy+2y2-18
e/x3-2020x2+2020x-2019
giúp em cần gấp ạ
Phân tích đa thức thành nhân tử:a)
x
2
- 8x + 7; b) 2
x
2
- 5x + 2;c)
x
4
+ 64; d)
(
8
-
2
x
2
)
2
- 18(x + 2)(x - 2).
Đọc tiếp
Phân tích đa thức thành nhân tử:
a) x 2 - 8x + 7; b) 2 x 2 - 5x + 2;
c) x 4 + 64; d) ( 8 - 2 x 2 ) 2 - 18(x + 2)(x - 2).