Quan sát hình 2.12 và hình 2.13, hãy cho biết các hướng của OA, OB, OC và OD có trong mỗi hình.
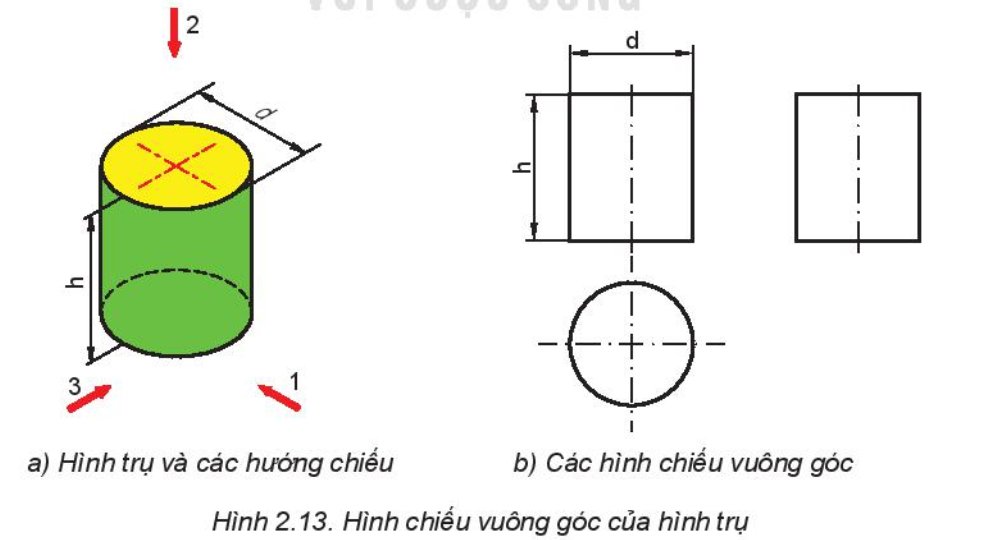
Quan sát Hình 2.13 và cho biết: Các hình chiếu vuông góc của hình trụ là hình gì? Có kích thước bằng bao nhiêu?
Tham khảo
- Hình chiếu đứng là hình chữ nhật, kích thước các cạnh là h, d
- Hình chiếu bằng là hình tròn, kích thước đường kính là d
- Hình chiếu cạnh là hình chữ nhật, kích thước các cạnh là h, d
Quan sát các hình từ 2.9 đến 2.12, em hãy cho biết các vật trong hình có đặc điểm gì khác nhau (sự trao đổi chất, khả năng sinh trưởng, phát triển và sinh sản).

Con gà, cây cà chua có sự trao đổi chất với môi trường, có sự sinh trưởng, lớn lên và có khả năng sinh sản ra thế hệ sau.
Đá sỏi và máy tính không có khả năng đó.
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi O là tâm hình vuông ABCD và điểm S thỏa mãn O S → = O A → + O B → + O C → + O D → + O A ' → + O B ' → + O C ' → + O D ' → . Tính độ dài đoạn OS theo a
A. OS=6a.
B. OS=4a.
C. OS=a.
D. OS=2a.
B1: Cho góc bẹt xOy. Trên cùng một nửa mặt phẳng bờ xy, vẽ các tia Om và On sao cho xOm=yOn và <90*. Gọi Oz là tia phân giác của góc mOn. Chứng minh rằng Oz _|_ xy.
B2: Cho góc AOB = 40*. Vẽ tia Oc là tia đối của tia OA. Tính góc COD, biết rằng:
a) OD _|_ Ob, các tia Od và OA thuộc hai nửa mặt phẳng đối nhau bờ Ob
b)OD _|_ Ob, các tia OD và OA thuộc cùng một nửa mặt phẳng bở OB
E CẦN GẤP MỌI NGƯỜI GIÚP E VS Ạ
CÓ HÌNH HOẶC HÌNH MINH HỌA THÌ CÀNG TỐT Ạ
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
31/ Cho hình bình hành ABCD có AC cắt BD tại O. Đáp án nào sau đây đúng:
A. OA = OB; OC = OD. B. OA = OD; OB = OC
C. OA = OC; OB = OD. D. AB = BC; CD = AD
32/ Hình vuông ABCD có chu vi bằng 36cm. Diện tích của hình vuông là:
A. 36cm2 B. 81cm3 C. 1296cm2 D. 81cm2
33/ Bác An có một mảnh vườn hình chữ nhật có chiều dài 72m, chiều rộng 40m. Bác An
muốn trồng các cây ăn trái xung quanh vườn sao cho mỗi góc vườn có một cây và khoảng
cách giữa hai cây là 4m. Số cây dùng để trồng là:
A. 60 cây B. 58 cây C. 56 cây D. 54 cây
Câu 31: C
Câu 32: D
Câu 33: C
GiuCho tg ABCD biết rằng tồn tại một điểm O sao cho các véctơ OA,OB,OC,OD(có mũi tên trên đầu nha) có độ dài bằng nhau và OA+OB+OC+OD= vécto 0 ( tất cả có mũi tên trên đầu hết nha). Cmr: ABCD là hình chữ nhật.
Giúp mình với.
Cho tứ giác ABCD , hai đường chéo AC và BD cắt nhau ở O. Biết rằng OA/OC=OB/OD hãy chứng minhABCD là hình thang có AB và CD là hai đáy
Đề bài yêu cầu chứng minh ABCD là hình thang có AB và CD là đáy. Vậy ta sẽ dựa trên đặc điểm của hình thang và chứng minh.Đặc điểm của hình thang là: Hình thang là hình có một cặp cạnh đối diện song song. Ở đây cặp cạnh đó chính là: hai đáy AB và CD (vì AB và CD luôn song song với nhau). Hơn nữa, hình thang này cũng đáp ứng được yêu cầu là: OA/OC =OB/OD (lưu ý:cách loại hình tứ giác khác cũng có thể đáp ứng yêu cầu này.Tuy nhiên ở đây mình ghi thêm để việc chứng minh ABCD là hình thang có AB và CD là hai đáy)
Ta sẽ thử cách loại hình tứ giác khác như : hình bình hành,hình vuông , hình chữ nhật,hình thoi,.v.v. Ta thấy rằng các loại hình này đều đáp ứng được yêu cầu là: OA/OC = OB/OD. Tuy nhiên các hình này lại không đáp ứng được yêu cầu là 1 cặp cạnh đối diện song song vì những hình này đều có 2 cặp cạnh đối diện song song,đó là những cặp cạnh sau: AB và CD ; AD và BC. Vì vậy,suy cho cùng thì chỉ có hình thang là đáp ứng được tất cả mọi yêu cầu của đề bài. Vậy là ta đã chứng minh được ABCD là hình thang có AB và CD là hai đáy.
Ở bài này vì mình giải thích các lí do để cho bạn dễ hiểu nên bài này sẽ hơi dài.Mong bạn thông cảm! Nếu bạn hiểu rõ rồi thì bạn có thể lược bỏ một số phần giải thích đi. Nhưng mà mình cũng phải nói với bạn rằng mình ko chắc đâu nha!
1. Cho AOB. Trong AOB vẽ OC, OD sao cho OC vuông góc OA, OB vuông góc OD. Tính COD
2. Cho góc tia AOB. Trong góc này vẽ 2 tia OC và OD lần lượt vuông góc với OA và OB
a. So sánh AOD và BOC
b. Vẽ OM là phân giác COD. Tia OM có phải là tia phân giác AOB không?
Vẽ hình luôn nha các bạn ( ^ o ^ )
Cho hình thang ABCD có AB // CD , hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD . Tìm khẳng định sai trong các khẳng định sau?
A. ABCD là hình thang cân
B. AC = BD
C. BC = AD
D. Tam giác AOD cân tại O.
* Ta có: OA = OB nên tam giác OAB cân tại O
* Do OC = OD nên tam giác OCD cân tại O
* vì OA = OB và OC = OD nên OA + OC = OB + OD
Hay AC = BD
Hình thang ABCD có hai đường chéo AC = BD nên đây là hình thang cân.
Suy ra: BC = AD và B A D ^ = A B C ^ ; A D C ^ = D C B ^
Chọn đáp án D
Bài 5: Cho 2 tia đối nhau OA, OB. Trên cùng 1 nửa mặt phẳng có bờ AB, vẽ các tia OC, OD sao cho AOC = 80 độ, BOD= 50 độ. Tia nào là tia phân giác của góc BOC. (Vẽ hình cho mik lun nha)
Bài 6: Trên cùng 1 nửa mặt phẳng có bờ chứa tia OA, vẽ các tia OB, OC sao cho AOB = 40 độ, AOC = 140 độ. Gọi OD là tia đối của tia OC. Hãy chứng tỏ rằng tia OA là tia phần giác của góc BOD. ( Vẽ hình giúp mik lun nha)