Trong không gian có bao nhiêu vị trí tương đối giữa 2 đường thẳng không đồng phẳng
DA
Những câu hỏi liên quan
Có bao nhiêu vị trí tương đối của 2 đường thẳng trong không gian?
A. 2
B. 3
C. 4
D. 5
Đáp án C
song song, cắt nhau, chéo nhau, trùng nhau
Đúng 0
Bình luận (0)
Cho hai đường thẳng phân biệt a và b trong không gian. Có bao nhiêu vị trí tương đối giữa a và b?
A. 3
B. 1
C. 2
D. 4
Đáp án A
Có 3 vị trí: chéo nhau, cắt nhau, song song
Đúng 0
Bình luận (0)
Cho hai đường thẳng phân biệt a và b trong không gian. Có bao nhiêu vị trí tương đối giữa a và b?
A. 3
B. 1
C. 2
D. 4
Đáp án A
Có 3 vị trí: chéo nhau, cắt nhau, song song
Đúng 0
Bình luận (0)
Cho hai đường thẳng phân biệt a và b trong không gian. Có bao nhiêu vị trí tương đối giữa a và b?
A. 1
B. 2
C. 3
D. 4
Cho đường thẳng a và mp (P) trong không gian. Có bao nhiêu vị trí tương đối của a và (P):
A. 1
B. 2
C. 3
D. 4
Đáp án C
Có 3 vị trí: Song song, nằm trên, cắt
Đúng 0
Bình luận (0)
Cho hai đường thẳng phân biệt cùng nằm trong một mặt phẳng. Có bao nhiêu vị trí tương đối giữa hai đường thẳng đó?
A. 1
B. 2
C. 3
D. 4
Đáp án C
Song song, cắt nhau, trùng nhau
Đúng 0
Bình luận (0)
Có bao nhiêu vị trí tương đối giữa đường thẳng và mặt phẳng?
A. 1
B. 2
C. 3
D. 4
Đáp án C
Có 3 vị trí tương đối giữa đường thẳng và mặt phẳng là: song song, cắt và đường thẳng nằm trong mặt phẳng
Đúng 0
Bình luận (0)
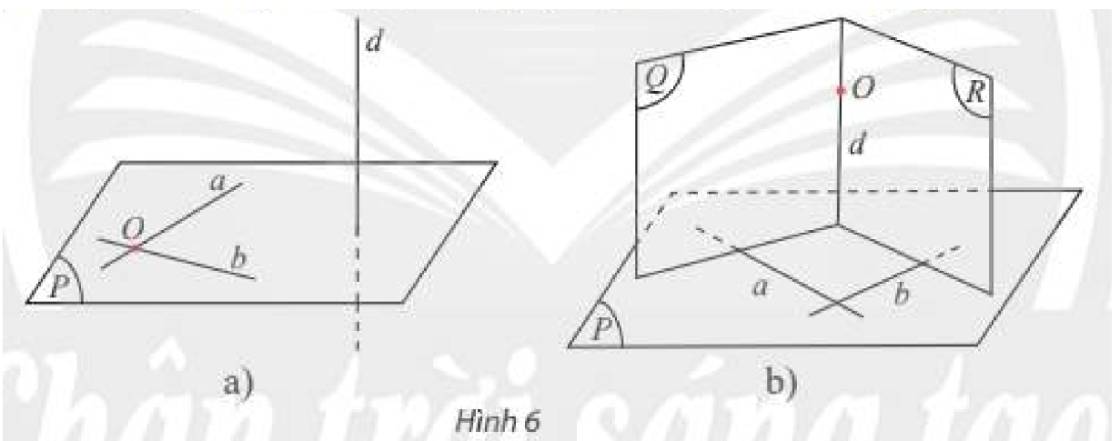
a) Trong không gian, cho điểm O và đường thẳng d. Gọi a,b là hai đường thẳng phân biệt đi qua O và vuông góc với d (Hình 6a). Có nhận xét gì về vị trí tương đối giữa đường thẳng d và mpleft( {a,b} right)?b) Trong không gian, cho điểm O và mặt phẳng left( P right). Gọi left( Q right) và left( R right) là hai mặt phẳng đi qua O và lần lượt vuông góc với hai đường cắt nhau a,b nằm trong left( P right) (Hình 6b). Có nhận xét gì về vị trí giữa mặt phẳng left( P right) và giao tuyến d của left( Q righ...
Đọc tiếp
a) Trong không gian, cho điểm \(O\) và đường thẳng \(d\). Gọi \(a,b\) là hai đường thẳng phân biệt đi qua \(O\) và vuông góc với \(d\) (Hình 6a). Có nhận xét gì về vị trí tương đối giữa đường thẳng \(d\) và \(mp\left( {a,b} \right)\)?
b) Trong không gian, cho điểm \(O\) và mặt phẳng \(\left( P \right)\). Gọi \(\left( Q \right)\) và \(\left( R \right)\) là hai mặt phẳng đi qua \(O\) và lần lượt vuông góc với hai đường cắt nhau \(a,b\) nằm trong \(\left( P \right)\) (Hình 6b). Có nhận xét gì về vị trí giữa mặt phẳng \(\left( P \right)\) và giao tuyến \(d\) của \(\left( Q \right),\left( R \right)\)?
tham khảo:
a) Vì đường thẳng d vuông góc hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) nên d⊥(P)
b) Vì a⊥(Q);d∈(Q) nên a⊥d
Vì b⊥(R),d∈(R) nên b⊥d
Vì đường thẳng d vuông góc hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) nên d⊥(P)
Đúng 1
Bình luận (0)
Trong không gian cho hai đường thẳng
d
1
:
x
-
1
-
2
y
+
2
1
z
-
4
3
và
d
2...
Đọc tiếp
Trong không gian cho hai đường thẳng d 1 : x - 1 - 2 = y + 2 1 = z - 4 3 và d 2 x + 1 1 = y - 1 = z + 2 3 . Xác định vị trí tương đối giữa d 1 , d 2 .
![]()
![]()
![]()
![]()




