(1 điểm) Dùng thước và compa vẽ hình thoi ABCD biết cạnh AB = 3cm, đường chéo AC = 5cm.
TA
Những câu hỏi liên quan
Dùng thước và compa vẽ hình thoi ABCD biết cạnh AB = 3cm, đường chéo AC = 5cm.
Dùng thước và compa vẽ hình theo cách diễn đạt sau:a) Vẽ tam giác ABC biết AB 5cm; BC 4cm; AC 3cm. Sau đó vẽ trung điểmcủa 3 cạnh tam giácb) Vẽ tam giác DEF biết D̂ 40°, DE 4cm; DF 5cm. Sau đó vẽ phân giác củaD̂, cắt cạnh đối diện tại Gc) Vẽ đường tròn tâm O bán kính 3cm, sau đó vẽ tam giác có độ dài các cạnhbằng bán kính của đường tròn và có một đỉnh là điểm O
Đọc tiếp
Dùng thước và compa vẽ hình theo cách diễn đạt sau:
a) Vẽ tam giác ABC biết AB = 5cm; BC = 4cm; AC = 3cm. Sau đó vẽ trung điểm
của 3 cạnh tam giác
b) Vẽ tam giác DEF biết D̂ = 40°, DE = 4cm; DF = 5cm. Sau đó vẽ phân giác của
D̂, cắt cạnh đối diện tại G
c) Vẽ đường tròn tâm O bán kính 3cm, sau đó vẽ tam giác có độ dài các cạnh
bằng bán kính của đường tròn và có một đỉnh là điểm O
Cho hình thoi ABCD. Gọi O là giao điểm của hai đường chéo, biết AB = 5cm và AO = 3cm. Diện tích hình thoi ABCD là:
A. 12 c m 2
B. 24 c m 2
C. 36 c m 2
D. 48 c m 2
Cho hình thoi ABCD, biết AB = 5cm, AI = 3cm (I là giao điểm của hai đường chéo). Hãy tính diện tích hình thoi.
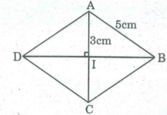
Áp dụng Pi-ta-go vào tam giác vuông IAB, ta có: A B 2 = A I 2 + I B 2
⇒ I B 2 = A B 2 - A I 2 = 25 – 9 = 16
⇒ IB = 4(cm).
AC = 2AI = 2.3 = 6 (cm)
BD = 2IB = 2.4 = 8 (cm)
S A B C D = 1/2 AC.BD = 1/2 .6.8 = 24 ( c m 2 )
Đúng 0
Bình luận (0)
Dựng hình thang ABCD (AB // CD), biết ba cạnh: AD = 2cm, CD = 4cm, BC = 3cm và đường chéo AC = 5cm.
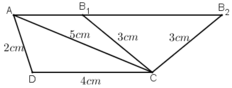
* Dựng hình:
- Dựng tam giác ADC có AD = 2cm, DC = 4cm, CA = 5cm.
- Dựng tia Ax song song với CD.
- Đường tròn (C; 3cm) cắt Ax tại B1 và B2.
Hình thang ABCD với B ≡ B1 hoặc B ≡ B2 là hình thang cần dựng.
* Chứng minh
+ Tứ giác ABCD có AD = 2cm, DC = 4cm, CA = 5cm.
+ Ax // CD ⇒ AB // CD ⇒ ABCD là hình thang.
+ B ∈ (C; 3cm) ⇒ BC = 3cm.
Đúng 0
Bình luận (0)
Cho hình thoi ABCD, biết AB = 5cm, AI = 3cm (I là giao điểm của hai đường chéo). Hãy tính diện tích hình thoi đó ?
Quan sát hình chữ nhật ở hình 4.8a.1. Nêu tên đỉnh, cạnh, đường chéo, hai cạnh đối của hình chữ nhật ABCD (h.4.8b).2. Dùng thước đo góc để đo và so sánh các góc của hình chữ nhật ABCD.3. Dùng thước thẳng hoặc compa để so sánh hai cạnh đối, hai đường chéo của hình chữ nhật ABCD.
Đọc tiếp
Quan sát hình chữ nhật ở hình 4.8a.
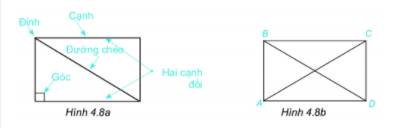
1. Nêu tên đỉnh, cạnh, đường chéo, hai cạnh đối của hình chữ nhật ABCD (h.4.8b).
2. Dùng thước đo góc để đo và so sánh các góc của hình chữ nhật ABCD.
3. Dùng thước thẳng hoặc compa để so sánh hai cạnh đối, hai đường chéo của hình chữ nhật ABCD.
1) Đỉnh: A, B, C, D
Cạnh: AB, BC, CD, DA
Đường chéo: AC, BD
Hai cạnh đối: AB và CD; BC và AD
2) Ta đo được: \(\widehat{A} = 90^0; \widehat{B} = 90^0; \widehat{C} = 90^0; \widehat{D} = 90^0\). Vậy các góc của hình chữ nhật đều bằng nhau và bằng 90o
3) Ta đo được: AB = CD ; AD = BC nên hai cạnh đối của hình chữ nhật bằng nhau
AC = BD nên hai đường chéo của hình chữ nhật bằng nhau.
Đúng 1
Bình luận (0)
Cho hình thoi ABCD có O là giao điểm của hai đường chéo. Biết OA 3cm và OB 5cm. Tính diện tích hình thoi? A. 30
c
m
2
B. 35
c
m
2
C. 40
c
m
2
D. 45
c
m
2
Đọc tiếp
Cho hình thoi ABCD có O là giao điểm của hai đường chéo. Biết OA = 3cm và OB = 5cm. Tính diện tích hình thoi?
A. 30 c m 2
B. 35 c m 2
C. 40 c m 2
D. 45 c m 2
VÌ ABCD là hình thoi nên O là trung điểm của AC và BD
Suy ra: AC = 2OA = 2.3 = 6cm
Và BD = 2.OB = 2.5= 10cm
Diện tích hình thoi là:
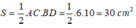
Chọn đáp án A
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có AB = 5cm ,DO =3cm .Đường chéo AC có độ dài bằng bao nhiêu?
O là tâm hình thoi đúng không nhỉ?
Do ABCD là hình thoi \(\Rightarrow AD=AB=5\left(cm\right)\)
Theo t/c hình thoi ta có tam giác ADO vuông tại O
Áp dụng định lý Pitago:
\(AO=\sqrt{AD^2-DO^2}=4\left(cm\right)\)
\(\Rightarrow AC=2AO=8\left(cm\right)\)
Đúng 1
Bình luận (0)





