do cac goc CED,CGD,BED,GCE
LC
Những câu hỏi liên quan
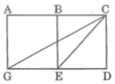
Đo các góc \(CED,CGD,BED,GCE\) ở hình 5

CED = 45 độ
CGD = 25 độ
BED = 90 độ
GCE = 65 độ
Đúng 0
Bình luận (0)
Đo các góc CED, CGD, BED, DCE ở hình dưới
Dùng thước đo góc, chúng ta đo được số đo các góc như sau:
Đúng 0
Bình luận (0)
Cho tam giac ABC co goc A =90 do . Tren cach BC lay diem E sao cho BE=BA.tia phan giac cua goc B cat canh AC tai D
a,So sanh do dai cac doan thang DA,DE
.b, Tinh so do goc BED
c, Chung minh BD vuong goc voi AE
D, So sanh so do cac goc ABC va goc CAE
cho tu giac abcd biet goc a: goc b: goc c: goc d =4:3:2:1
a) tinh cac goc cua tu giac abcd
b) cac tia phan giac cua goc c va goc d cat nhau tai e. cac duong phan giac cua goc ngoai tai ca dinh c va d cat nhau tai f. tinh goc ced va goc cfd
a) Ta có: \(\frac{\widehat{A}}{4}=\frac{\widehat{B}}{3}=\frac{\widehat{C}}{2}=\frac{\widehat{D}}{1}\)
Áp dụng t/c dãy tỉ số bằng nhau ta được:
\(\frac{\widehat{A}}{4}=\frac{\widehat{B}}{3}=\frac{\widehat{C}}{2}=\frac{\widehat{D}}{1}=\frac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{4+3+2+1}=\frac{360}{10}=36\)
\(\Rightarrow\widehat{A}=144^0;\widehat{B}=108^0;\widehat{C}=72^0;\widehat{D}=36^0\)
Cho tu giac ABCD co goc A = 1000, B = 1200 , cac tia phan giac cua goc C va D cat nhau tai E.
a) Tinh CED
b) Cac tia phan giac cua goc ngoai tai dinh C va D cat nhau tai F. Chung minh: \(\widehat{CED}+\widehat{CFD}=180^0\)
Cho tu giac ABCD co A = 1000 , B = 1200 , cac tia phan giac cua C va D cat nhau tai E
a) Tinh goc CED
b) Cac tia phan giac cua goc ngoai tai dinh C va D cat nhau tai F. Chung minh: CED + CFD = 1800
Cho tam giac ABC co goc A khac goc B cac tia phan giac trong va ngoai cua goc C lan luot cat duong thang BA tai D va E tinh goc CED theo goc A va goc B cua tam giac ABC
cho tam giac ABC cac tia phan giac trong va phan giac ngoia cua goc C cat duong thang AB lan luot o D va E tinh goc CED theo goc A va goc Bcua tam giac ABC
tu giac ABCD co : goc A= 65 , goc B = 117
cac tia p/g cua goc C va D cat nhau tai E . cac duong p/g cua cac goc ngoai tai dinh C va D cat nhau tai F . Tinh goc CED , CFD ?
- ve hinh , giai ?
giup gium e vs mai phai nop r ![]()

