giải phương trình sau
12x = 13y + 12x
tìm x ,y
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao:
a ) y = 3 − 2 x y = 3 x − 1 b ) y = − 1 2 x + 3 y = − 1 2 x + 1 c ) 2 y = − 3 x 3 y = 2 x d ) 3 x − y = 3 x − 1 3 y = 1
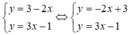
a) Xét (d): y = -2x + 3 có a = -2; b = 3
(d’) : y = 3x – 1 có a’ = 3 ; b’ = -1.
Có a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ 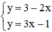 có nghiệm duy nhất.
có nghiệm duy nhất.
b) 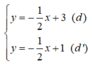
Xét (d): 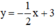 có a =
có a = 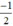 ; b = 3
; b = 3
(d’): 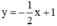 có a’ =
có a’ = 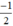 ; b’ = 1.
; b’ = 1.
Có a = a’; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ phương trình 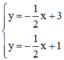 vô nghiệm.
vô nghiệm.
c) Ta có: 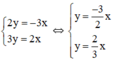
Xét (d): y = 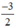 x có a =
x có a = 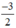 ; b = 0
; b = 0
(d’) : y = 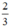 x có a’ =
x có a’ = 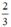 ; b’ = 0
; b’ = 0
Ta có: a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ 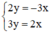 có nghiệm duy nhất.
có nghiệm duy nhất.
d) Ta có:
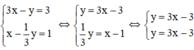
Ta có: a = a’=3; b = b’ = -3
Nhận thấy hai đường thẳng trên trùng nhau
⇒ Hệ phương trình có vô số nghiệm.
Kiến thức áp dụng
+ Xét hệ (I): 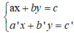
Gọi (d): ax + by = c và (d’): a’x + b’y = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’.
Giải các phương trình nghiệm nguyên:
a) 12x + 13y = 156
b) 3xy - x - y = 1
c) x3- y3= 91
giải hệ phương trình bằng cả phép thế và cộng đại số:
\(\hept{\begin{cases}8x-7y=5\\12x+13y=-8\end{cases}}\)
Cả hai à tham thế i:
Cộng Đại Số
\(\hept{\begin{cases}8x-7y=5\\12x+13y=-8\end{cases}\Leftrightarrow\hept{\begin{cases}24x-21y=15\left(1\right)\\24x+26y=-16\left(2\right)\end{cases}}}\)
Lấy (2) trừ (1)
\(\left(24x-24x\right)-21y-26y=15-\left(-16\right)\)
\(\Leftrightarrow47y=-31\Rightarrow y=\frac{31}{47}\)thay vào đầu x=5+7.31/47
Giải hệ phương trình bằng cả phép thế và cộng đại số:
\(\hept{\begin{cases}8x-7y=5\\12x+13y=-8\end{cases}}\)
dùng máy tính í
shift 5 1 rồi nhạp giá trị
giống hệt bài của nguyễn thị phương thảo
\(8x-7y=5\Leftrightarrow48x-42y=30\)(1)
\(12x+13y=-8\Leftrightarrow48x+52y=-32\)(2)
trừ 1 2 theo vế \(\Leftrightarrow-94y=62\)
giải nốt
1.Cho 12x2+13y2=25xy
Tính \(P=\dfrac{x+y}{x-y}\)
2.Giải phương trình: x3-2x+1=0
2/
\(x^3-2x+1=0\)
\(\Rightarrow x^3-x-x+1=0\)
\(\Rightarrow x\left(x^2-1\right)-\left(x-1\right)=0\)
\(\Rightarrow x\left(x-1\right)\left(x+1\right)-\left(x-1\right)=0\)
\(\Rightarrow\left(x-1\right)\left(x^2+x-1\right)\)
\(\Rightarrow x=1\)
Vậy S = {1}
Giải các hệ phương trình sau bằng phương pháp thế: 3 x + 5 y = 1 2 x - y = - 8
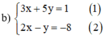
Từ (2) ta rút ra được y = 2x + 8 (*)
Thế (*) vào phương trình (1) ta được :
3x + 5(2x + 8) = 1 ⇔ 3x + 10x + 40 = 1 ⇔ 13x = -39 ⇔ x = -3.
Thay x = - 3 vào (*) ta được y = 2.(-3) + 8 = 2.
Vậy hệ phương trình có nghiệm duy nhất (-3 ; 2).
\(\text{Giải hệ phương trình sau:}\left\{{}\begin{matrix}x^2+y^2+3=4x\\x^3+12x+y^3=6x^2+9\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x^2+y^2+3=4x\\x^3+12x+y^3=6x^2+9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x^2-4x+4\right)+y^2=1\\\left(x^3-6x^2+12x-8\right)+y^3=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-2\right)^2+y^2=1\\\left(x-2\right)^3+y^3=1\end{matrix}\right.\)
Đặt \(a=x-2;b=y\). Hệ phương trình trở thành:
\(\left\{{}\begin{matrix}a^2+b^2=1\\a^3+b^3=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2ab=\left(a+b\right)^2-1\\\left(a+b\right)\left(a^2+b^2-ab\right)=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2ab=\left(a+b\right)^2-1\\\left(a+b\right)\left(1-\dfrac{\left(a+b\right)^2-1}{2}\right)=1\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\left(a+b\right)\left[3-\left(a+b\right)^2\right]=2\)
\(\Leftrightarrow3\left(a+b\right)-\left(a+b\right)^3=2\)
\(\Leftrightarrow\left(a+b\right)^3-3\left(a+b\right)+2=0\)
\(\Leftrightarrow\left(a+b\right)^3-\left(a+b\right)^2+\left(a+b\right)^2-\left(a+b\right)-2\left(a+b-1\right)=0\)
\(\Leftrightarrow\left(a+b\right)^2\left(a+b-1\right)+\left(a+b\right)\left(a+b-1\right)-2\left(a+b-1\right)=0\)
\(\Leftrightarrow\left(a+b-1\right)\left[\left(a+b\right)^2+\left(a+b\right)-2\right]=0\)
\(\Leftrightarrow\left(a+b-1\right)^2\left(a+b+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=1\\a+b=-2\end{matrix}\right.\)
Với \(\left\{{}\begin{matrix}a+b=1\\a^2+b^2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=1\\\left(a+b\right)^2-2ab=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=1\\ab=0\end{matrix}\right.\)
\(\Rightarrow\left(a;b\right)=\left(0;1\right),\left(1;0\right)\)
\(\Rightarrow\left(x-2;y\right)=\left(0;1\right),\left(1;0\right)\)
\(\Rightarrow\left(x;y\right)=\left(2;1\right),\left(3;0\right)\)
Với \(\left\{{}\begin{matrix}a+b=-2\\a^2+b^2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=-2\\\left(a+b\right)^2-2ab=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=-2=S\\ab=\dfrac{3}{2}=P\end{matrix}\right.\left(2\right)\)
Ta có: \(S^2-4P=\left(-2\right)^2-4.\dfrac{3}{2}=-2< 0\)
\(\Rightarrow\)Không tồn tại số a,b nào thỏa hệ phương trình (2).
Vậy nghiệm (x;y) của hpt đã cho là \(\left(2;1\right),\left(3;0\right)\)
Giải các bất phương trình sau bằng 1 2 x < x - 1 2
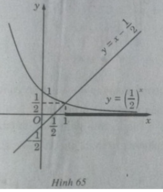
Vẽ đồ thị của hàm số 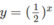 và đường thẳng
và đường thẳng 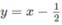 trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số
trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số 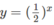 nằm phía dưới đường thẳng
nằm phía dưới đường thẳng 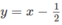 . Vậy tập nghiệm của bất phương trình đã cho là (1;+
∞
)
. Vậy tập nghiệm của bất phương trình đã cho là (1;+
∞
)
Giải các bất phương trình sau: x + 1 2 x - 1 + x ≤ 3 + 2 x 2