Tìm x lớn nhất thỏa mãn: 2.|x+9|=10
CH
Những câu hỏi liên quan
Tìm x lớn nhất thỏa mãn : 2.[x+9] = 10 . Trả lời x =
2.|x+9| = 10
|x+9|=5
mà x lớn nhất
=>x+9=5
=>x=-4
Đúng 0
Bình luận (0)
2.|x+9| = 10
|x+9|=5
mà x lớn nhất
=>x+9=5
=>x=-4
Đúng 0
Bình luận (0)
2.[x+9] = 10
[x+9] = 10:2
[x+9] = 5
Vậy x+9 = 5 hoặc x + 9 = -5
Nên x=-4 hoặc x= -14
Mà x lớn nhất => x = -4
K cho mình nhé !!! Chúc bạn học tốt !!!! >.<
Đúng 0
Bình luận (0)
Tìm số lớn nhất thỏa mãn: 2.|x+9|=10. Trả lời: x=
2 . |x + 9| = 10
=> 2 . (x + 9) = 10 hoặc 2 . (x + 9) = -10
=> x + 9 = 10 : 2 hoặc x + 9 = -10 : 2
=> x + 9 = 5 hoặc x + 9 = -5
=> x = 5 - 9 hoặc x = -5 - 9
=> x = -4 hoặc x = -14
Mà x lớn nhất.
=> x = -4
Đúng 0
Bình luận (0)
2.| x + 9 | = 10
=> | x + 9 | = 10 : 2
=> | x + 9 | = 5 <=> x + 9 = ± 5
TH1 : x + 9 = 5 => x = 5 - 9 => x = - 4 ( chọn )
TH2 : x + 9 = - 5 => x = - 5 - 4 => x = - 9 ( chọn )
Vì x lớn nhấn nên x = - 4
Đúng 0
Bình luận (0)
Cho x,y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y
+
2
x
x
-...
Đọc tiếp
Cho x,y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x x - 9 + y y - 9 + x y . Tìm giá trị lớn nhất của biểu thức P = 3 x + 2 y - 9 x + y - 10 khi x,y thay đổi.
A. 2
B. 3
C. 1
D. 0
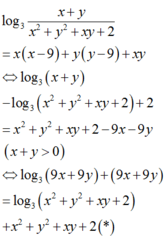

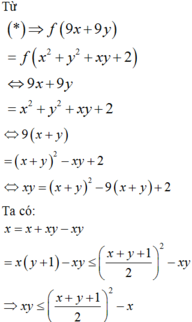
Từ đó
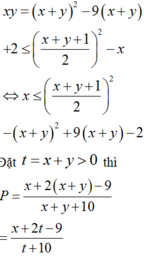
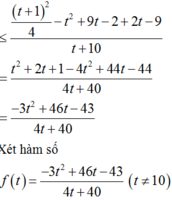
Sử dụng MTCT ta tìm được max P = 2 .
Chọn A.
Đúng 0
Bình luận (0)
Cho x là số tự nhiên lớn nhất thỏa mãn : 5 và x/10 < 25/4
A. x=10 B. x=9 C. x=12 D. x=13
Cho các số thực x,y thỏa mãn : x^2/9 + y^2/16 = 36 . Tìm giá trị nhỏ nhất và giá trị lớn nhất P = x - y + 2020
Cho các số thực x,y thỏa mãn : x^2/9 + y^2/16 = 36 . Tìm giá trị nhỏ nhất và giá trị lớn nhất P = x - y + 2020
Cho các số thực x,y thỏa mãn : x^2/9 + y^2/16 = 36 . Tìm giá trị nhỏ nhất và giá trị lớn nhất P = x - y + 2020
Cho số thực x, y thỏa mãn hệ thức: x^2+2xy+7x+7y+2y^2+10=0. Hãy tìm giá tri lớn nhất, nhỏ nhất của: S=x+y+1.
Cho x,y là các số thực dương thỏa mãn x+y+xy=3 tìm các giá trị lớn nhất của biểu thức
\(P=\sqrt{9-x^2}+\sqrt{9-y^2}+\dfrac{x+y}{4}\)
\(3=x+y+xy\le\sqrt{2\left(x^2+y^2\right)}+\dfrac{x^2+y^2}{2}\)
\(\Rightarrow\left(\sqrt{x^2+y^2}-\sqrt{2}\right)\left(\sqrt{x^2+y^2}+3\sqrt{2}\right)\ge0\)
\(\Rightarrow x^2+y^2\ge2\)
\(\Rightarrow-\left(x^2+y^2\right)\le-2\)
\(P=\sqrt{9-x^2}+\sqrt{9-y^2}+\dfrac{x+y}{4}\le\sqrt{2\left(9-x^2+9-y^2\right)}+\dfrac{\sqrt{2\left(x^2+y^2\right)}}{4}\)
\(P\le\sqrt{2\left(18-x^2-y^2\right)}+\dfrac{1}{4}.\sqrt{2\left(x^2+y^2\right)}\)
\(P\le\left(\sqrt{2}-1\right)\sqrt{18-x^2-y^2}+\sqrt[]{2}\sqrt{\dfrac{\left(18-x^2-y^2\right)}{2}}+\dfrac{1}{2}\sqrt{\dfrac{x^2+y^2}{2}}\)
\(P\le\left(\sqrt{2}-1\right).\sqrt{18-2}+\sqrt{\left(2+\dfrac{1}{4}\right)\left(\dfrac{18-x^2-y^2+x^2+y^2}{2}\right)}=\dfrac{1+8\sqrt{2}}{2}\)
Dấu "=" xảy ra khi \(x=y=1\)
Đúng 2
Bình luận (0)





