Cho tam giác ABC , điểm M là điểm nằm trên phân giác ngoài của góc C . Chứng minh MA + MB > AC + AC
NT
Những câu hỏi liên quan
cho tam giác ABC , M là điểm trên tia phân giác của góc ngoài đỉnh C. Chứng minh rằng MA + MB > AC + BC
Cho tam giác ABC. Điểm M nằm trên đường phân giác của góc ngoài đỉnh C. Chứng minh AC + CB < AM + MB
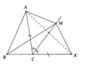
Trên tia đối của tia CB lấy điểm A' sao cho CA' = CA. Sử dụng tính chất của tam giác cân ta có được CM là đường trung trực của AA' Þ MA = MA'. Sử dụng bất đẳng thức trong tam giác A'MB ta có: CA + CB = CA' + CB = BA' <MA' + MB Þ CA + CB < MA + MB.
Đúng 0
Bình luận (0)
Cho tam giác ABC. Điểm M nằm trên đường phân giác của góc ngoài đỉnh C (M khác C). Chứng minh rằng AC+ CB < AM+ MB
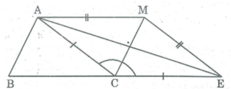
Trên tia đối tia CB lấy điểm E sao cho CE = CA. Nối MA, ME nên ∆ ACE cân tại C có CM là đường phân giác nên CM là đường trung trực (tính chất tam giác cân)
⇒ MA = ME (tính chất đường trung trực)
Ta có: AC + BC = CE + BC = BE (1)
MA + MB = ME + MB (2)
Trong ∆ MBE, ta có: BE < MB+ ME (bất đẳng thức tam giác) (3)
Từ (1), (2) và (3) suy ra: AC + CB < AM + MB.
Đúng 0
Bình luận (0)
Cho tam giác ABC . Điểm M nằm trên đường phân giác của góc ngoài đỉnh C( M khác C ) . Chứng minh AC + CB < AM +MB .

⇒" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:16.38px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal; word-wrap:normal" class="MathJax_CHTML mjx-chtml"> MA + MB > BC + AC (đpcm)
Đúng 0
Bình luận (0)
Mình cá luôn là hai người này đều lấy từ trên mạng ra và bài toán này cũng từ trên mạng ra.
Đúng 0
Bình luận (0)
Cho tam giác ABC . Điểm M nằm trên đường phân giác của góc ngoài đỉnh C( M khác C ) . Chứng minh AC + CB < AM +MB .

Từ A kẻ đường vuông góc với tia pg của góc ngoài đỉnh C và cắt tia đối của tia CB tại A'.
C/m được MA = MA', CA = CA'.
Áp dụng BĐT vào tam giác MBA' :
MA' + MB > BA' = BC + CA' = BC + AC
⇒ MA + MB > BC + AC (đpcm)
Đúng 0
Bình luận (0)
cho tam giác ABC .Điểm M nằm trên đường phân giác của góc ngoài đỉnh C (M khác C ).Chứng minh rằng AC+CB<AM+MB
gọi d là đường phân giác của góc ngoài tại C trên tia đối của tia Cb lấy E sao cho CE=CA
vì tam giác ACE cân tại C d là đường phân giác của góc ACE nên d là đường trung trực của AEdo đó MA=ME
ta có AC+CB=EC+CB=BE
AM+MB=EM+MB
tâm giác BME có BE<EM+MB
=> AC+CB<AM+MB
mk chỉ có thể vẽ hình minh họa
Đúng 0
Bình luận (0)
cho tam giác ABC, M là điểm trên tia phân giác ngoài của góc C. CMR MA+MB>AC+AB
Bài 3. Cho tam giác ABC, điểm M nằm trên tia phân giác ngoài của góc C (M không
trùng với C). Chứng minh MA + MB > CA + CB.
Cho tam giác ABC có M thuộc tia phân giác ngoài của góc C. Trên tia đối của tia CA lấy điểm I sao cho CI=CB.
a) So sánh MI với MB.
b) Chứng minh MA+MB<AC+BC
a)
Xét∆BCM = ∆ICM ( c-g-c )
=) BM=MI
b)
Ta có BM=MI
=) MA+MB=MA+MI . (1)
Lai có BC=IC
=) AC+BC = AC+IC=AI . (2)
Xét∆AMI có AM+MI>AI ( bđt ∆ ). (3)
Từ (1);(2);(3)=) MA+MB>AC+BC
Đúng 0
Bình luận (0)
Các bạn cho mình xin hình vẽ được không ạ?
Đúng 0
Bình luận (0)
Ko biết ve hinh sao cho đep trên máy cả.
Tự túc đi nha!
.
Đúng 0
Bình luận (0)

