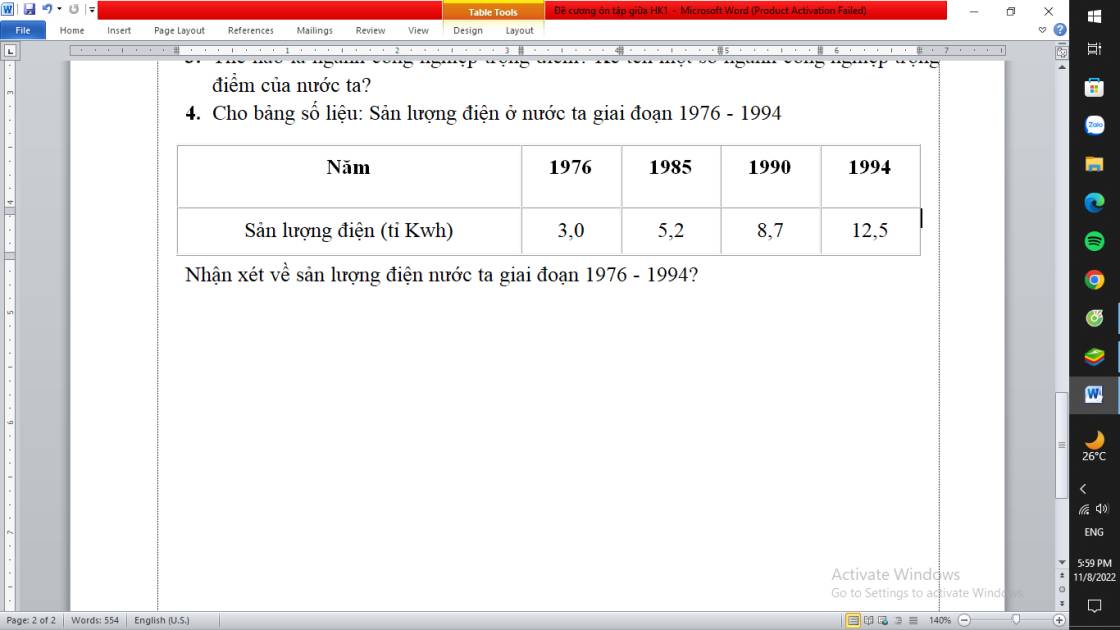
giúp e bài 4 với ạaa
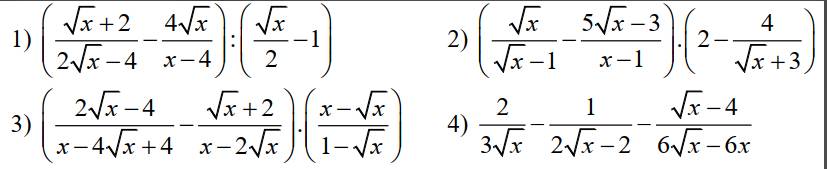 giúp e bài này với ạaa
giúp e bài này với ạaa
1: \(=\left(\dfrac{\sqrt{x}+2}{2\left(\sqrt{x}-2\right)}-\dfrac{4\sqrt{x}}{x-4}\right):\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{x+4\sqrt{x}+4-8\sqrt{x}}{2\left(x-4\right)}\cdot\dfrac{2}{\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)^2\cdot\left(\sqrt{x}+2\right)}=\dfrac{1}{\sqrt{x}+2}\)
3: \(=\dfrac{x+\sqrt{x}-5\sqrt{x}+3}{x-1}\cdot\dfrac{2\sqrt{x}+6-4}{\sqrt{x}+3}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{2\left(\sqrt{x}+1\right)}{\sqrt{x}+3}=\dfrac{2\left(\sqrt{x}-3\right)}{\sqrt{x}+3}\)
giúp mjnk bài 1 và 4 với ạaa
GIÚP EM CÂU B BÀI 4 VÀ BÀI 5 VỚI ẠAA,EM CẦN GẤPP
Bài 5:
a: Để đây là hàm số bậc nhất thì m+5<>0
hay m<>-5
giải giúp e 3 bài này ạaa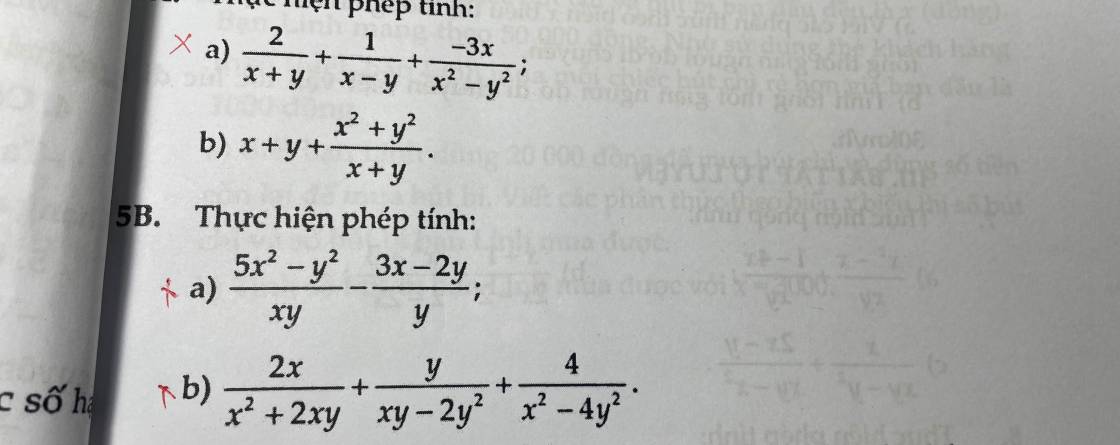
a1/\(\dfrac{2}{x+y}+\dfrac{1}{x-y}+\dfrac{-3x}{x^2-y^2}\)
\(=\dfrac{2\left(x-y\right)}{\left(x+y\right)\left(x-y\right)}+\dfrac{x+y}{\left(x+y\right)\left(x-y\right)}+\dfrac{-3x}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{2x-2y+x+y-3x}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{-y}{\left(x+y\right)\left(x-y\right)}\)
a2/\(\dfrac{5x^2-y^2}{xy}-\dfrac{3x-2y}{y}\)
\(=\dfrac{5x^2-y^2}{xy}-\dfrac{3x^2-2xy}{xy}\)
\(=\dfrac{5x^2-y^2-3x^2+2xy}{xy}\)
\(=\dfrac{2x^2-y^2+2xy}{xy}\)
b/\(\dfrac{2x}{x^2+2xy}+\dfrac{y}{xy-2y^2}+\dfrac{4}{x^2-4y^2}\)
\(=\dfrac{2x}{x\left(x+2y\right)}+\dfrac{y}{y\left(x-2y\right)}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{2}{x+2y}+\dfrac{1}{x-2y}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{2\left(x-2y\right)}{\left(x-2y\right)\left(x+2y\right)}+\dfrac{x+2y}{\left(x-2y\right)\left(x+2y\right)}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{2x-4y+x+2y+4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{3x-2y+4}{\left(x-2y\right)\left(x+2y\right)}\)
#TienDatzZz
a) \(\dfrac{2}{x+y}+\dfrac{1}{x-y}+\dfrac{-3x}{x^2-Y^2}\)
\(\dfrac{2\left(x-y\right)}{\left(x+y\right)\left(x-y\right)}+\dfrac{\left(x+y\right)}{\left(x+y\right)\left(x-y\right)}+\dfrac{-3x}{x^2-y^2}\)
\(\dfrac{2x-2y+x+y-3x}{x^2-y^2}\)
\(\dfrac{-y}{x^2-y^2}\)
Giúp e với ạaa
1 education
2 scientific
3 discover
4 Tragically
5 safety
 giúp e với ạaa
giúp e với ạaa
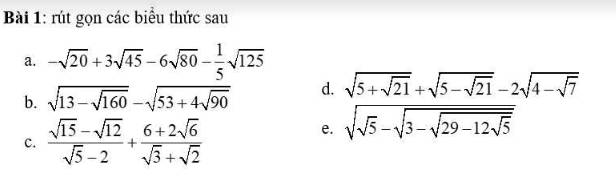 giúp e với ạaa
giúp e với ạaa
 giúp e gấp với ạaa
giúp e gấp với ạaa
Xét ΔABC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
Xét (B;BA) có
BA là bán kính
CA vuông góc BA tại A
Do đó: CA là tiếp tuyến của (B;BA)
 giúp e gấp với ạaa
giúp e gấp với ạaa
Xét ΔABC có
BE,CF là đường phân giác
BE cắt CF tại I
Do đó: I là tâm đường tròn nội tiếpΔABC
=>d(I;BC)=d(I;AB)=d(I;AC) và AI là phân giác của góc BAC
ΔABC cân tại A
mà AI là phân giác
nên AI vuông góc BC tại D
=>d(I;BC)=ID
=>d(I;AB)=d(I;AC)=ID
=>AB,AC là tiếp tuyến của (I;ID)

giúp e gấp với ạaa
Bài 2:
a: Xét (O) có
CM,CA là tiếp tuyến
Do đó: CM=CA và OC là phân giác của \(\widehat{AOM}\)
Xét (O) có
DM,DB là tiếp tuyến
Do đó: DM=DB và OD là phân giác của \(\widehat{BOM}\)
\(\widehat{AOM}+\widehat{BOM}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
b: CD=CM+MD
mà CM=CA và DM=DB
nên CD=CA+DB
c: Xét ΔOCD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
=>\(AC\cdot BD=OM^2=R^2\) không đổi