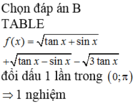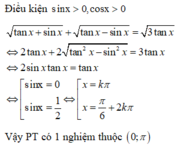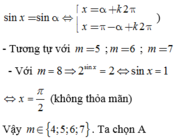số nghiệm của phương trình sin3x + sinx = 0 trong khoảng (-π/2; π) là
HL
Những câu hỏi liên quan
Phương trình sin 3 x + cos 2 x – sin x = 0 có tập nghiệm (0; π) là:
A. {π/4;3π/4}
B. {π/4}
C. {3π/4}
D. {π/6;π/4;3π/4}
Chọn A
Ta có sin3x+ cos2x- sinx= 0 ⇔ cos2x(2sinx+1)=0. Lưu ý trong khoảng (0;π), sinx > 0
Đúng 0
Bình luận (0)
Số nghiệm thuộc khoảng
0
;
π
của phương trình
tan
x
+
sin
x
+
tan
x
−
sin
x
3
tan
x
là. A. 0 B. 1. C. 2 D. 3
Đọc tiếp
Số nghiệm thuộc khoảng 0 ; π của phương trình tan x + sin x + tan x − sin x = 3 tan x là.
A. 0
B. 1.
C. 2
D. 3
Đáp án B
TABLE f ( x ) = tan x + sin x + tan x − sin x − 3 tan x đổi dấu 1 lần trong 0 ; π ⇒ 1 nghiệm
Đúng 0
Bình luận (0)
Số nghiệm thuộc khoảng
0
;
π
của phương trình
tan
x
+
sin
x
+
tan
x
-
sin
x
3
tan
x
là A. 0. B. 1. C. 2. D. 3.
Đọc tiếp
Số nghiệm thuộc khoảng 0 ; π của phương trình tan x + sin x + tan x - sin x = 3 tan x là
A. 0.
B. 1.
C. 2.
D. 3.
Số nghiệm thuộc khoảng
0
;
π
của phương trình.
tan
x
+
sin
x
tan
x
-
sin
x
3
tan
x
là A. 0. B. 1 C. 2. D. 3.
Đọc tiếp
Số nghiệm thuộc khoảng 0 ; π của phương trình. tan x + sin x = tan x - sin x = 3 tan x là
A. 0.
B. 1
C. 2.
D. 3.
Đáp án B
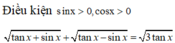
![]()
![]()
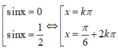
Vậy PT có 1 nghiệm thuộc (0; π )
Đúng 0
Bình luận (0)
Số nghiệm thuộc khoảng
0
;
π
của phương trình.
tan
x
+
sin
x
+
tan
x
-
sin
x
3
tan
x
là A. 0. B. 1 C. 2. D. 3
Đọc tiếp
Số nghiệm thuộc khoảng 0 ; π của phương trình.
tan x + sin x + tan x - sin x = 3 tan x là
A. 0.
B. 1
C. 2.
D. 3
Cho phương trình:
(
sin
x
+
sin
3
x
+
cos
3
x
1
+
2
sin
2
x
)
3
+
cos
2
x
5...
Đọc tiếp
Cho phương trình: ( sin x + sin 3 x + cos 3 x 1 + 2 sin 2 x ) = 3 + cos 2 x 5 . Các nghiệm của phương trình thuộc khoảng ( 0 ; 2 π ) là:
![]()
![]()
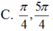
![]()

![]()

![]()
Vì các nghiệm của phương trình thuộc khoảng
(
0
;
2
π
)
nên nghiệm của phương trình là ![]()
Đúng 0
Bình luận (0)
Số nghiệm của phương trình sinx+cosx=1 trên khoảng (0;π) là
A. 0
B. 1
C. 2
D. 3
Địt mẹ mày, sao đéo thấy đáp án đâu, web đầu buồi
Đúng 0
Bình luận (0)
Tìm tổng các giá trị nguyên của tham số m để phương trình
4
sin
x
+
2
1
+
sin
x
m
có tổng các nghiệm trong khoảng
0
;
π
bằng
π
A. 22 B. 25 C. 30 D. 33
Đọc tiếp
Tìm tổng các giá trị nguyên của tham số m để phương trình 4 sin x + 2 1 + sin x = m có tổng các nghiệm trong khoảng 0 ; π bằng π
A. 22
B. 25
C. 30
D. 33
Tìm tổng các giá trị nguyên của tham số m để phương trình
4
sin
x
+
2
1
+
sin
x
m
có tổng các nghiệm trong khoảng
0
;
π
bằng
π
. A. 22 B. 25 C. 30 D. 33
Đọc tiếp
Tìm tổng các giá trị nguyên của tham số m để phương trình 4 sin x + 2 1 + sin x = m có tổng các nghiệm trong khoảng 0 ; π bằng π .
A. 22
B. 25
C. 30
D. 33
Đáp án A
Điều kiện x ∈ ℝ
Đặt t = 2 sin x . Phương trình đã cho trở thành t 2 + 2 t = m ( * )
Vì sin x = sin α ⇔ x = α + 2 k π x = π − α + k 2 π nên để phương trình đã cho có tổng các nghiệm trong khoảng 0 ; π bằng π thì phương trình (*) phải có đúng một nghiệm t ∈ 1 ; 2 sin x ∈ 0 ; 1 thì 2 sin x ∈ 1 ; 2
Xét hàm số f t = t 2 + 2 t có bảng biến thiên
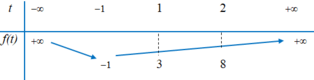
Suy ra để phương trình (*) có đúng một nghiệm t ∈ 1 ; 2 thì m ∈ 3 ; 8 .Vậy tổng các giá trị nguyên của m thỏa mãn yêu cầu bài toán là 4 + 5 + 6 + 7 = 22
Đúng 0
Bình luận (0)
Số nghiệm của phương trình
sin
x
sin
2
x
+
2
sin
x
cos
2
x
+
sin
x
+
cos
x
sin
x
+...
Đọc tiếp
Số nghiệm của phương trình sin x sin 2 x + 2 sin x cos 2 x + sin x + cos x sin x + cos x = 3 cos 2 x trong khoảng − π ; π là:
A. 2
B. 4
C. 3
D. 5
Đáp án A
DK: sin x + cos x ≠ 0 ⇔ tan x ≠ − 1 ⇔ x ≠ − π 4 + k π
Khi đó P T ⇔ sin x sin 2 x + sin 2 x cos x + sin x + cos x sin x + cos x = 3 cos 2 x
⇔ sin x + cos x sin 2 x + 1 sin x + cos x = 3 cos 2 x − sin 2 x ⇔ sin 2 x − 2 sin x cos x + cos 2 x = 3 sin x + cos x cos x − sin x ⇔ sin x + cos x sin x + cos x = 3 sin x + cos x cos x − sin x ⇔ sin x + cos x = 3 cos x − sin x ⇔ 1 + 3 sin x = 3 − 1 cos x ⇔ tan x = 3 − 1 1 + 3 ⇔ x = π 12 + k π
có 2 nghiệm thuộc − π ; π
Đúng 0
Bình luận (0)