cHO TAM GIÁC abc VUÔNG TẠI a. cẠNH ab= 5CM đường cao AH, BH= 3CM, CH=8 cm. Tính AC.
YS
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có AB=3cm, BC=5cm. AH là đường cao. Tính cạnh BH, CH, AC và AH
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=16\)
hay AC=4cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=1.8cm\\CH=3.2cm\\AH=2.4cm\end{matrix}\right.\)
Đúng 1
Bình luận (0)
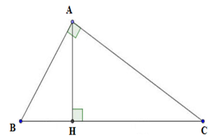
Xét tam giác ABC vuông tại A
+ Theo định lý Pytago ta có:
+ Theo hệ thức lượng trong tam giác vuông ta có:
A B 2 = BH. BC => BH = A B 2 B C = 3 2 5 = 9 5 = 1 , 8 c m
Mà BH + CH = BC => CH = BC – BH = 5 – 1,8 = 3,2 cm
Lại có AH. BC = AB.AC => AH = A B . A C B C = 3.4 5 = 2,4cm
Vậy BH = 1,8cm, CH = 3,2cm, AC = 4cm, AH = 2,4 cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Cạnh AB= 5cm đường cao AH, BH= 3cm, CH= 8cm. Tính AC
Cho tam giác ABC vuông tại A. Cạnh AB =5cm đường cao AH, BH= 3cm, CH= 8cm. Tính AC
ta có BH + HC = BC ( vì điểm H nằm giữa B và C )
hay 3 + 8 = BC
suy ra BC = 11
áp dụng định lý pi ta go thì bạn sẽ tìm ra AC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Cạnh AB= 5cm đường cao AH, BH= 3cm, CH= 8cm. Tính AC.
nếu bạn đã học định lí Py-ta-go rồi thì ta có: AB\(^2\)+ AC\(^2\)=BC\(^2\)
5\(^2\)+ AC \(^2\)= 121
AC = \(\sqrt{96}\)
NHỚ BẤM ĐÚNG CHO MÌNH NHÉ!
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC cân tại B, kẻ CH vuông góc AB. Biết AH= 1cm, BH= 4cm. Tính độ dài AC.
Bài 2: Cho tam giác ABC vuông tại A. Cạnh AB= 5cm đường cao AH, BH= 3cm, CH= 8cm. Tính AC.
Bài 3: Cho tam giác ABC vuông tại A, có \(\frac{AB}{BC}=\frac{3}{5}\)và AC= 16cm. Tính độ dài các cạnh AB=BC.
Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
Đúng 0
Bình luận (0)
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB 3cm, BC 5cm. AH là đường cao. Tính BH, CH, AC và AH. A. BH 2cm, CH 3,2cm, AC 4cm, AH 2,4cm B. BH 1,8cm; CH 3,2cm; AC 4cm; AH 2,4cm C. BH 1,8cm; CH 3,2cm; AC 3cm; AH 2,4cm D. BH 1,8cm; CH 3,2cm; AC 4cm; AH 4,2cm
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = 3cm, BC = 5cm. AH là đường cao. Tính BH, CH, AC và AH.
A. BH = 2cm, CH = 3,2cm, AC = 4cm, AH = 2,4cm
B. BH = 1,8cm; CH = 3,2cm; AC = 4cm; AH = 2,4cm
C. BH = 1,8cm; CH = 3,2cm; AC = 3cm; AH = 2,4cm
D. BH = 1,8cm; CH = 3,2cm; AC = 4cm; AH = 4,2cm

Xét tam giác ABC vuông tại A
+ Theo định lý Pytago ta có:
![]()
+ Theo hệ thức lượng trong tam giác vuông ta có:
A B 2 = BH. BC => BH = A B 2 B C = 3 2 5 = 9 5 = 1 , 8 c m
Mà BH + CH = BC => CH = BC – BH = 5 – 1,8 = 3,2 cm
Lại có AH. BC = AB.AC => AH = A B . A C B C = 3.4 5 = 2,4cm
Vậy BH = 1,8cm, CH = 3,2cm, AC = 4cm, AH = 2,4 cm
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A . AB/AC = 8/15 và BC 17 cm , đường cao AH . Tính các cạnh tam giác ABC và AH , CH , BH
Áp dụng định lí pi ta go
=> AB2 + AC2 = 289
Mà \(\dfrac{AB}{AC}\) = \(\dfrac{8}{15}\)=> (\(\dfrac{AB}{AC}\))2 = \(\dfrac{64}{225}\)
=> AC2=225 => AC = 15 => AB = 8
Ta có: AB.AC=BC . AH
=> AH = 120/17=7.06
=>BH = 3.76
=> CH = 13.24
Đúng thì like giúp mik nha bạn. Thx bạn
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH
a, Cho biết AB = 3cm, BC = 5cm. Tính độ dài đoạn thẳng BH,CH, AH và AC
b, Cho biết AH = 60cm, CH = 144cm. Tính độ dài đoạn thẳng AB, AC, BC, và BH
a, HB = 1,8cm; CH = 3,2cm; AH = 2,4cm; AC = 4cm
b, AB = 65cm; AC = 156cm; BC = 169cm; BH = 25cm
c, AB = 5cm; BC = 13cm; BH = 25/13cm; CH = 144/13cm
Đúng 0
Bình luận (0)
1.cho tam giác ABC vông tại A, đường cao AH. Biết AB=3cm, BC=5cm. Tính AC, AH, BH, CH 2. Cho tam giác ABC vông tại A, đường cao AH. Biết HB=3,6cm, HC=6,4cm. Tính BC,AB,AC,AH
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=5^2-3^2=16\)
hay AC=4cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{3^2}{5}=1.8\left(cm\right)\\CH=\dfrac{4^2}{5}=3.2\left(cm\right)\end{matrix}\right.\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot5=3\cdot4=12\)
hay AH=2,4cm
Đúng 1
Bình luận (0)
Bài 2:
Ta có: BC=HB+HC
nên BC=3,6+6,4
hay BC=10cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=3.6\cdot10=36\\AC^2=6.4\cdot10=64\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=6\left(cm\right)\\AC=8\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AH^2=6^2-3.6^2=23.04\)
hay AH=4,8cm
Đúng 1
Bình luận (0)






