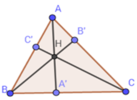
Cho tam giác ABC, đường cao AA';BB';CC',H là trực tâm tam giác
a,Tính tổng\(\frac{HA'}{AA'}\)+\(\frac{HB'}{BB'}\)+\(\frac{HC'}{CC'}\)
b,AI là phân giác tam giác ;IM;IN là phân giác AIC;AIB.Chứng minh rằng :AN*BI*CM=BN*IC*AM
c,Tam giác ABC thế nào thì\(\frac{\left(AB+BC+CA\right)^2}{AA'^2+BB'^2+CC'^2}\)nhỏ nhất