Với a thuộc z . hãy so sánh a2 với 2a
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
TH
Những câu hỏi liên quan
Với a thuộc Z. Hãy so sánh a2 và 2a.
Làm nhanh hộ mình nhé.
bạn ơi gửi giúp mình đáp án đầy đủ nhé
Đúng 0
Bình luận (0)
ta co 2a=a+a,a mu 2=a.a.suy ra a mu 2 >2a (mk chi nghi vay thoi)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
với a thuộc z so sánh a^2 và 2a
TH1: a Là số âm ta có:
\(a^2\ge0\)với mọi a
\(2a< 0\)với mọi a
\(\Rightarrow a^2>2a\)
TH2: \(a=1\)
\(\Rightarrow a^2< 2a\left(1< 2\right)\)
TH3:\(a=0;a=2\)
\(\Rightarrow a^2=2a\left(4=4hoặc0=0\right)\)
TH4:\(a\ge3\)
\(\Rightarrow a^2>2a\)
VẬY:\(a^2>2a\)Khi \(a< 0;a\ge3\)
\(a^2=2a\)Khi \(a=0;a=2\)
\(a^2< 2a\)Khi \(a=1\)
Đúng 0
Bình luận (0)
Với a \(\in\) Z. Hãy so sánh a2 và 2a.
Có đủ 3 trường hợp:
+) a2 = 2a khi a = 0 hoặc 2
Giải cụ thể:
a2 = 2a => a2 - 2a = 0
=> a(a-2) = 0 => a = 0;2
+) a2 > 2a khi a > 2 hoặc a < 0
+) a2 < 2a khi 0 < a < 2
Với \(A\in Z\), Hãy so sánh \(a^2\)và \(2a\)
TH1: a^2=2a
TH2:a^2>2a
với \(a\in Z\)
Xét 3 trường hợp
Khi a< 0 thì a2 > 2a ( 1 )
Khi a = 0, 1 , 1 thì a2 = 2a ( 2 )
Khi a> 2 thì a2 > 2a ( 3 )
Từ ( 1) , ( 2 ) , ( 3 ) \(\Rightarrow a^2\ge2a\)
a2 =a.a
a có thể lớn hơn hoặc = 2
=>a2 sẽ lớn hơn hoặc = a.2
Học tốt !
Xem thêm câu trả lời
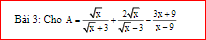
a. Rút gọn A
b. Tính giá trị A khi x = 64
c. Tìm x để 2A = 1
d. Tìm x để A < 1
e. So sánh A với 0,5
f. Tìm GTLN của A
g. Tìm x thuộc Z để A nguyên
h.Tìm x để A nguyên
k.Tìm m để 2A = m
Giúp mình những câu mik in đậm nhé
Thanks mọi người
Đúng 0
Bình luận (0)
a) ĐKXĐ: \(x\ge0,x\ne9\)
\(A=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3}{\sqrt{x}+3}\)
b) \(A=\dfrac{3}{\sqrt{x}+3}=\dfrac{3}{\sqrt{64}+3}=\dfrac{3}{8+3}=\dfrac{3}{11}\)
c) \(2A=\dfrac{6}{\sqrt{x}+3}=1\Rightarrow\sqrt{x}+3=6\Rightarrow x=9\left(tm\right)\)
g) \(A=\dfrac{3}{\sqrt{x}+3}\in Z\)
\(\Rightarrow\sqrt{x}+3\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
Kết hợp đk:
\(\Rightarrow x\in\left\{0\right\}\)
h) \(A=\dfrac{3}{\sqrt{x}+3}\in Z\)
\(\Rightarrow\sqrt{x}+3\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
Kết hợp đk:
\(\Rightarrow x\in\left\{0\right\}\)
k) \(2A=\dfrac{6}{\sqrt{x}+3}=m\)
Đúng 1
Bình luận (2)
Với a, b, c bất kỳ. Hãy so sánh a2 + b2 + c2 và ab + bc + ca? A. a2 + b2 + c2 ab + bc + ca B. a2 + b2 + c2 ≥ ab + bc + ca C. a2 + b2 + c2 ≤ ab + bc + ca D. a2 + b2 + c2 ab + bc + ca
Đọc tiếp
Với a, b, c bất kỳ. Hãy so sánh a2 + b2 + c2 và ab + bc + ca?
A. a2 + b2 + c2 = ab + bc + ca
B. a2 + b2 + c2 ≥ ab + bc + ca
C. a2 + b2 + c2 ≤ ab + bc + ca
D. a2 + b2 + c2 > ab + bc + ca
Xét hiệu:
a2 + b2 + c2 - ab - bc - ca
= 1 2 (2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ca)
= 1 2 [(a2 - 2ab + b2) + (b2 - 2bc + c2) + (c2 - 2ca + a2)]
= 1 2 [(a - b)2 + (b - c)2 + (c - a)2] ≥ 0
(vì (a - b)2 ≥ 0; (b - c)2 ≥ 0; (c - a)2 ≥ 0 với mọi a, b, c)
Nên a2 + b2 + c2 ≥ ab + bc + ca.
Dấu “=” xảy ra khi a = b = c.
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Với a, b, c bất kỳ. Hãy so sánh 3(a2 + b2 + c2) và (a + b + c)2 A. 3(a2 + b2 + c2) (a + b + c)2 B. 3(a2 + b2 + c2) ≤ (a + b + c)2 C. 3(a2 + b2 + c2) ≥ (a + b + c)2 D. 3(a2 + b2 + c2) (a + b + c)2
Đọc tiếp
Với a, b, c bất kỳ. Hãy so sánh 3(a2 + b2 + c2) và (a + b + c)2
A. 3(a2 + b2 + c2) = (a + b + c)2
B. 3(a2 + b2 + c2) ≤ (a + b + c)2
C. 3(a2 + b2 + c2) ≥ (a + b + c)2
D. 3(a2 + b2 + c2) < (a + b + c)2
Xét hiệu:
3(a2 + b2 + c2) - (a + b + c)2
= 3a2 + 3b2 + 3c2 - a2 - b2 - c2 - 2ab - 2bc - 2ac
= 2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ac
= (a - b)2 + (b - c)2 + (c - a)2 ≥ 0
(vì (a - b)2 ≥ 0; (b - c)2 ≥ 0; (c - a)2 ≥ 0 với mọi a, b, c
Nên 3(a2 + b2 + c2) ≥ (a + b + c)2.
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
cho x thuộc Z, hãy so sánh x2 với x3
Khi x là số nguyên dương thì x2<x3
Khi x là số nguyên âm thì x2>x3
Khi x là số 0 thì x2=x3
Đúng 0
Bình luận (0)
có 3 trường hợp:
TH1: Nếu x thuộc Z- thì x2>x3
TH2: Nẽu x thuộc Z+ thì x2<x3
TH3: Nếu x là 0 thì x2=x3
Đúng 0
Bình luận (0)
Nếu x là số nguyên dương thì x2 < x3
Nếu x là số nguyên âm thì x2 > x3
Nêu x = 0 thì x2 = x3
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho a < b, hãy so sánh: 2a +1 với 2b + 1
a < b
⇒ 2a < 2b (nhân hai vế với 2 > 0, BĐT không đổi chiều)
⇒ 2a + 1 < 2b + 1 (cộng hai vế với 1).
Vậy 2a + 1 < 2b + 1.
Đúng 0
Bình luận (0)


