b: Xét tứ giác AECF có 

AE//CF

AE=CF

Do đó: AECF là hình bình hành

Suy ra: FA//CE

a: BE=AB/2

DF=DC/2

mà AB=DC

nên BE=DF

Xét tứ giác BEDF có

BE//DF

BE=DF

=>BEDF là hình bình hành

=>DE=BF

b: BEDF là hbh

=>BD cắt EF tại trung điểm của mỗi đường(1)

ABCD là hbh

=>AC cắt BD tại trung điểm của mỗi đường(2)

Từ (1), (2) suy ra AC,BD,EF đồng quy

Ta có: 

tam giác AEB = tam giác CFD 

=> \(\widehat{AEB}=\widehat{CFD}=\widehat{EDF}\left(slt\right)\) 

mà 2 goác có vị trí đồng vị

=> EB//DF

Mặt khác: ED//BF

=> EBFD là h.b.h

Ta có: 

Tam giác END= tam giác FMB

=> DN=BM

=> DN+MN=BM+MN=BN

Ta có:

Vì tứ giác ABCD và EBFC đều là h.b.h

=> AC, BD, EF đồng quy tại trung điểm của EF

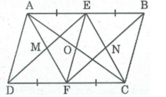
+) Ta có:

AE = 1/2 AB; CF = 1/2. CD ( vì E và F lần lượt là trung điểm của AB, CD).

Và AB = CD (tính chất hình bình hành)

Suy ra: AE = CF

+) Lại có: AB // CD ( vì ABCD là hình bình hành) nên AE //CF

Tứ giác AECF có hai cạnh đối AE, CF song song và bằng nhau nên là hình bình hành

⇒ AF //CE hay EN // FM (1)

Xét tứ giác BFDE ta có:

AB // CD (gt) hay BE // DF

BE = 1/2 AB (gt)

DF = 1/2 CD (gt)

AB = CD (tính chất hình bình hành)

Suy ra: BE = DF

Tứ giác BFDE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ BF//DE hay EM // FN (2)

Từ (1) và (2) suy ra tứ giác EMFN là hình bình hành (theo định nghĩa hình bình hành)

chắc là AF//CD Á

af//cd có nghĩa là gì vậy

af//dc thì khác j af//cd

trời ơi trời

Xét tứ giác AECF có

AE//CF

AE=CF

Do đó: AECF là hình bình hành

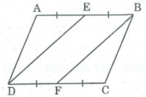
Ta có: AB = CD (tính chất hình bình hành)

EB = 1/2 AB (gt)

FD = 1/2 CD (gt)

Suy ra: EB = FD (1)

Mà AB // CD (gt)

⇒ BE // FD (2)

Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

⇒ DE = BF (tính chất hình bình hành)

Lời giải:

a. Vì $ABCD$ là hình bình hành nên $AB=CD$

$\Rightarrow \frac{1}{2}AB=\frac{1}{2}CD$
$\Rightarrow AF=CE(1)$

Mặt khác: $AB\parallel CD\Rightarrow AF\parallel CE(2)$

Từ $(1); (2)\Rightarrow AECF$ là hình bình hành.

b. 

B, E,F thẳng hàng??? Bạn xem lại đề.

t cung chưa làm đc đm