\(M=x^2+4x+10\)

\(=\left(x^2+4x+4\right)+6\)

\(=\left(x+2\right)^2+6\ge6\).

Vậy: \(MinM=6\). Dấu đẳng thức xảy ra khi và chỉ khi \(x+2=0\Leftrightarrow x=-2.\)

`M = x^2 + 4x + 4 + 6 = (x+2)^2 + 6 >= 0 + 6  =6`.

ĐTXR `<=> x + 2 = 0 <=> x = -2`.

Vậy Min M = `6 <=> x = -2`.

1, Ta có: 3-x²+2x=-(x²-2x+1)+4=-(x-1)²+4

vì (x-1)² luôn lớn hơn hoặc bằng không với mọi x-->-(x-1)² nhỏ hơn hoặc bằng 0 với mọi x

vậy giá trị lớn nhất của biểu thức 3-x²+2x là 4

các bài giá trị  nhỏ nhất còn lại làm tương tự bạn nhé

chỉ cần đưa về nhân tử chung hoặc hằng đẳng thức là được

1 . 

3−x2+2x3−x2+2x

=−(x2−2x−3)=−(x2−2x−3)

=−(x2−2.x.1+1−4)=−(x2−2.x.1+1−4)

=−((x−1)2−4)=−((x−1)2−4)

=4−(x−1)2≤4=4−(x−1)2≤4

Vậy MAXB=4⇔x−1=0⇒x=1

2 . 

A=2x2−5x+2=2(x2−52x+2516)−98A=2x2−5x+2=2(x2−52x+2516)−98

=2(x−54)2−98=2(x−54)2−98

Ta có : 2(x−54)2≥0∀x;2(x−54)2−98≥−98∀x2(x−54)2≥0∀x;2(x−54)2−98≥−98∀x

Vậy GTNN A = -9/8 <=> x = 5/4 

3 . 

Điều kiện x ≠ 2 và x  ≠  0

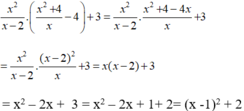
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.

Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.

Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.

B3:\(\Rightarrow90.10^n-10^n.10^2+10^n.10-20\Rightarrow10^n.\left(90-10^2\right)+10^n.10-20\)

\(\Rightarrow10^n.\left(90-100\right)+10^n.10-20\Rightarrow-10.10^n+10^n.10-20\Rightarrow-20\)

\(A=-\left(x^2-x+5\right)=-\left(x^2-2.\frac{1}{2}x+\frac{1}{4}+\frac{19}{4}\right)=-\left[\left(x-\frac{1}{2}\right)^2+\frac{19}{4}\right]\)

\(=-\left(x-\frac{1}{2}\right)^2-\frac{19}{4}\le-\frac{19}{4}\)

Vậy \(A_{min}=-\frac{19}{4}\Leftrightarrow x-\frac{1}{2}=0\Rightarrow x=\frac{1}{2}\)

B2: \(\Rightarrow16x^2-8x-\left(16x^2-8x+1\right)-13\Rightarrow16x^2-8x-16x^2+8x-1-13\Rightarrow-14\)

a) gtnn bạn ạ

GTNN A=  -4 vì 2/3x-1/ >= 0

b) gtln bạn ạ

GTLN B = 10 vì 4/x-2/ >=0

A= -4; B= 10

a: Ta có: \(A=\left(x-1\right)\left(x-3\right)+11\)

\(=x^2-4x+3+11\)

\(=x^2-4x+4+8\)

\(=\left(x-2\right)^2+8\ge8\forall x\)

Dấu '=' xảy ra khi x=2

b: Ta có: \(B=-4x^2+4x+5\)

\(=-\left(4x^2-4x+1-6\right)\)

\(=-\left(2x-1\right)^2+6\le6\forall x\)

Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)

a, \(A=-x^2-2x+3=-\left(x^2+2x-3\right)=-\left(x^2+2x+1-4\right)\)

\(=-\left(x+1\right)^2+4\le4\)

Dấu ''='' xảy ra khi x = -1 

Vậy GTLN là 4 khi x = -1 

b, \(B=-4x^2+4x-3=-\left(4x^2-4x+3\right)=-\left(4x^2-4x+1+2\right)\)

\(=-\left(2x-1\right)^2-2\le-2\)

Dấu ''='' xảy ra khi x = 1/2 

Vậy GTLN B là -2 khi x = 1/2 

c, \(C=-x^2+6x-15=-\left(x^2-2x+15\right)=-\left(x^2-2x+1+14\right)\)

\(=-\left(x-1\right)^2-14\le-14\)

Vâỵ GTLN C là -14 khi x = 1

Bài 8 : 

b, \(B=x^2-6x+11=x^2-6x+9+2=\left(x-3\right)^2+2\ge2\)

Dấu ''='' xảy ra khi x = 3

Vậy GTNN B là 2 khi x = 3 

c, \(x^2-x+1=x^2-x+\dfrac{1}{4}+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)

Dấu ''='' xảy ra khi x = 1/2 

Vậy ...

c, \(x^2-12x+2=x^2-12x+36-34=\left(x-6\right)^2-34\ge-34\)

Dấu ''='' xảy ra khi x = 6

Vậy ...

\(A=10x^2+6xy+y^2-4x+3\)

\(A=9x^2+6xy+y^2+x^2-4x+4-1\)

\(A=\left(3x+y\right)^2+\left(x-2\right)^2-1\)

Có: \(\left(3x+y\right)^2+\left(x-2\right)^2\ge0\)

\(\Rightarrow\left(3x+y\right)^2+\left(x-2\right)^2-1\ge-1\)

Dấu = xảy ra khi: \(\left(3x+y\right)^2+\left(x-2\right)^2=0\)

\(\Rightarrow\hept{\begin{cases}\left(3x+y\right)^2=0\\\left(x-2\right)^2=0\end{cases}}\Rightarrow\hept{\begin{cases}3x+y=0\\x-2=0\end{cases}}\Rightarrow\hept{\begin{cases}3x+y=0\\x=2\end{cases}}\Rightarrow\hept{\begin{cases}6+y=0\\x=2\end{cases}}\Rightarrow\hept{\begin{cases}y=-6\\x=2\end{cases}}\)

Vậy: \(Min_A=-1\) tại \(\hept{\begin{cases}y=-6\\x=2\end{cases}}\)

a) Ta có: \(\left|x-2\right|\ge0\forall x\)

\(\Leftrightarrow\left|x-2\right|+15\ge15\forall x\)

Dấu '=' xảy ra khi x=2

b) Ta có: \(\left|x-5\right|\ge0\forall x\)

\(\Leftrightarrow2\left|x-5\right|\ge0\forall x\)

\(\Leftrightarrow2\left|x-5\right|-4\ge-4\forall x\)

Dấu '=' xảy ra khi x=5