cho f(x)=x2017-2016x2016-2016x2015-...-2016x-1
Tính f(2015)
NN
Những câu hỏi liên quan
Cho f(x)=x^2017-2016x^2016+2016x^2015-...+2016x-1. Tính f(2015)
Theo đề bài ta có
\(f\left(x\right)=x^{2017}-2016.x^{2016}+2016.x^{2015}-...+2016.x-1\)
Với \(f\left(2015\right)\)thì \(x=2015,x+1=2016\)
\(\Rightarrow f\left(x\right)=x^{2017}-\left(x+1\right).x^{2016}+\left(x+1\right).x^{2015}-...+\left(x+1\right).x-1\)
\(\Rightarrow f\left(x\right)=x^{2017}-x^{2017}-x^{2016}+x^{2016}+x^{2015}-...+x^2+x-1\)
\(\Rightarrow f\left(x\right)=x-1\)
\(\Rightarrow f\left(2015\right)=2015-1=2014\)
Vậy f(2015)=2014
Đúng 0
Bình luận (0)
f(x)=x^2015-2016x^2014+2016x^2012+...-2016x^2+2016x-1
cho đa thức F(x) =\(x^{25}-2016x^{24}+2016x^{23}-2016x^{22}+......+2016x-1\)
tính giá trị biểu thức tại x=2015
Cho đa thức :
f(x)=x^2017 - 2016.x^2016 - 2016.x^2015 - ... - 2016x + 1
f(x)= x^2017 - 2016.x^2016 - 2016.x^2015 - ... - 2016x + 1
f(x)= x^2017 - (2017 - 1)x^2016 - (2017 - 1)x^2015 - ... - (2017 - 1)x +1
Với x=2017 ta có :
f(x)= x^2017 - (x - 1)x^2016 - (x-1)x^2015 - ... - (x - 1)x +1
f(x)= x^2017 - x^2017 +x^2016 - x^2016 +...+ x^2 - x^2 + x + 1
f(x)= x + 1
Thay x =2017 vào f(x) ta có :
f(2017) = 2017 +1 = 2018
Đúng 0
Bình luận (0)
Cho đa thức:
\(f\left(x\right)=x^6-2016x^5+2016x^4-2016x^3+2016x^2-2016x+4032\)
Tính f (2018)
\(x=2018\Rightarrow2016=x-2\)
\(\Rightarrow f\left(x\right)=x^6-\left(x-2\right)x^5+\left(x-2\right)x^4-\left(x-2\right)x^3+\left(x-2\right)x^2-\left(x-2\right)x+2x\)
\(\Rightarrow f\left(x\right)=x^6-x^6+2x^5+x^5-2x^4-x^4+2x^3+x^3-2x^2-x^2-2x+2x\)
\(\Rightarrow f\left(x\right)=3x^5-3x^4+3x^3-3x^2\)
\(\Rightarrow f\left(x\right)=3x^2\left(x^3-x^2+x-1\right)\)
\(\Rightarrow f\left(2018\right)=3.2018^2\left(2018^3-2018^2+2017\right)\)
Nói thật luôn là bn xem đề thế nào đi chứ mình cứ thấy có j đó sai sai ở đây
Đúng 0
Bình luận (0)
Cho đa thức
\(f\left(x\right)=x^6-2016x^5+2016x^4-2016x^3+2016x^2-2016x\) \(+4032\)
Tính f(2018)
cảm ơn bạn đã ra câu hỏi cho mình , chờ mình giải nhé bạn
f(x) = x ^ 6 - 2016x ^ 5 + 2016x^4 - ... - 2016x + 4032
= x ^6 - 2017x^5 +x^5 + 2017x^4 -...- 2017x + x + 4032
= x^5 ( x - 2017 ) - x^4 ( x - 2017 ) +...- x (x -2017 ) + x + 4032
=> f ( 2018 ) = x^5 - x^4 + x^3 - x^2 + 2x + 4032
= 2018^5 - 2018^4 +2018^3 - 2018^2 + 12096
* KL *
nhầm r , chuyển 12096 thành 8064
Cho hàm số f(x) có đạo hàm trên R thỏa mãn
f
(
x
)
-
2018
f
(
x
)
2018
.
2017
.
x
2017
.
e
2018
x
với mọi
x
∈
R
;
f
(
0
)
2018
.
Giá trị của f(1) là A. ...
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên R thỏa mãn f ' ( x ) - 2018 f ( x ) = 2018 . 2017 . x 2017 . e 2018 x với mọi x ∈ R ; f ( 0 ) = 2018 . Giá trị của f(1) là
A. f ( 1 ) = 2018 e - 2018
B. f ( 1 ) = 2019 e - 2018
C. f ( 1 ) = 2018 e 2018
D. f ( 1 ) = 2019 e 2018
Cho hàm số f(x) có đạo hàm trên
ℝ
thỏa mãn f’(x) – 2018f(x) 2018.x2017.e2018x với mọi
x
∈
ℝ
và f(0) 2018. Tính giá trị f(1). A. f(1) 2019e2018. B. f(1) 2018e-2018. C. f(1) 2018e2018. D. f(1) 2017e2018.
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên ℝ thỏa mãn f’(x) – 2018f(x) = 2018.x2017.e2018x với mọi x ∈ ℝ và f(0) = 2018. Tính giá trị f(1).
A. f(1) = 2019e2018.
B. f(1) = 2018e-2018.
C. f(1) = 2018e2018.
D. f(1) = 2017e2018.
Chọn A
Lấy tích phân từ 0 đến 1 của 2 vế:
Đúng 0
Bình luận (0)
Cho hàm số y f(x) thỏa mãn
∫
0
π
2
sin
x
f
(
x
)
d
x
f
(
0
)
1
Tính
∫
0
π
2
cos
x
.
f
(
x
)...
Đọc tiếp
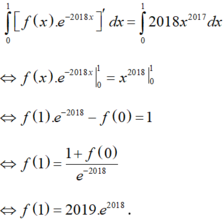
Cho hàm số y =f(x) thỏa mãn ∫ 0 π 2 sin x f ( x ) d x = f ( 0 ) = 1 Tính ∫ 0 π 2 cos x . f ' ( x ) d x
A. I = 2
B. I = -1
C. I = 1
D. I = 0
