2x+1 =3 và y-2=3( phải viết 4 trường hợp)
LV
Những câu hỏi liên quan
Tính góc giữa hai đường thẳng ∆1 và ∆2 trong trường hợp sau: Δ1: 2x + y – 4 = 0 và Δ2 : 5x – 2y + 3 = 0.
Hai đường thẳng Δ1 và Δ2 có vecto pháp tuyến lần lượt là: n1→(2;1); n2→(5;-2)
Góc giữa hai đường thẳng (Δ1) và (Δ2) là:
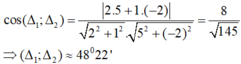
Đúng 1
Bình luận (0)
11. Viết pt đường thẳng \(d\) trong các trường hợp sau
a. \(d\) đi qua \(M\left(2;-3\right)\) và song song với \(d_1:y=-2x+5;\)
b. \(d\) đi qua \(N\left(-1;-2\right)\) và vuông góc với \(d_2:y=-x-8;\)
a: (d)//(d1)
=>(d): y=-2x+b
Thay x=2 và y=-3 vào (d), ta được:
b-4=-3
=>b=1
b: Vì (d) vuông góc (d2)
nên (d): y=x+b
Thay x=-1 và y=-2 vào (d), ta được:
b-1=-2
=>b=-1
Đúng 0
Bình luận (0)
viết phương trình đường thẳng d trong các trường hợp sau:
a) d đi qua điểm A nằm trên Ox có hoành độ bằng -3 và song song với đường thẳng d1 : y=-5x+4
b) d vuông góc với đường thẳng d2 : y=-1/2x +2018 và đi qua giao điểm của d3 : y=-x+3
Tìm x,y,z trong các trường hợp sau
a) \(\frac{1}{2}.x=\frac{2}{3}.y=\frac{3}{4}.z\)và x-y=15
b) 4x=3y,5y=4z và 2x+3y+5z=86
b)Ta có: 4x=3y =) x/3=y/4
5y=4z =) y/4=z/5
Do đó suy ra: x/3=y/4=z/5 =) 2x/6=3y/12=5z/25
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
2x/6=3y/12=5z/25=2x+3y+5z/6+12+25=86/43=2
=) 2x/6=2=)x=6; 3y/12=2=)y=8; 5z/25=2=)z=10
Vậy x=6; y=8; z=10
Đúng 0
Bình luận (0)
ban do lam dung roi do
k tui nha
thanks
Đúng 0
Bình luận (0)
Viết phương trình đường thẳng ; Vẽ đồ thị và tính khoảng cách
giữa 2 điểm với các trường hợp sau:
1) A(4; 1) và B(3; 4)
2) M(1; 2) và N(6; 1)
3) P(1; 6) và Q(3; 3)
giúp mình bài này với mai mình phải nôp rùi .huhu
tìm các cặp (x,y) thỏa mãn đồng thời
a.x+y=5 và |x+1|+|y-2| =4
b.x-y=3 và |x-6|+|y-1| =4
c.x-y=2 và|2x+1|+|2y+1| =4
d.2x+y=3 và |2x+3|+|y+2| =8
a>x+y=5=> y=5-x
\(!x+1!+!3-x!\ge!x+1+3-x!=4\)
đẳng thức khi -1<=x<=3
=> xem lại đề
Đúng 0
Bình luận (0)
Tính số đo góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trong môi trường hợp sau:
a) \({\Delta _1}:\left\{ \begin{array}{l}x = - 3 + 3\sqrt 3 t\\y = 2 + 3t\end{array} \right.\) và \({\Delta _2}:y - 4 = 0\)
b) \({\Delta _1}:2x - y = 0\) và \({\Delta _2}: - x + 3y - 5 = 0\)
a) - Ta có: \(\overrightarrow {{u_1}} = \left( {3\sqrt 3 ;3} \right);\overrightarrow {{u_2}} = \left( {1 ;0} \right) \Rightarrow \cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right)} \right| = \frac{{\left| {3\sqrt 3 .1 + 3.0} \right|}}{{\sqrt {{{\left( {3\sqrt 3 } \right)}^2} + {3^2}} .\sqrt {{1^2} + {0^2}} }} = \frac{{\sqrt 3 }}{2}.\)
- Vậy \(\left( {{\Delta _1},{\Delta _2}} \right) = {30^o}\)
b) – Ta có\(\overrightarrow {{n_1}} = \left( {2; - 1} \right);\overrightarrow {{n_2}} = \left( { - 1 ;3} \right) \Rightarrow \cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {2.\left( { - 1} \right) + \left( { - 1} \right).3} \right|}}{{\sqrt {{{\left( 2 \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{{\left( 1 \right)}^2} + {3^2}} }} = \frac{{\sqrt 2 }}{2}.\)
- Vậy \(\left( {{\Delta _1},{\Delta _2}} \right) = {45^o}\)
Đúng 0
Bình luận (0)
điểm M (4; 5) thuộc đường thảng nào trong các trường hợp sau đây
A y = 3x -4
B y +2x = 1
C 2x-y =3
D y-x = -2
Tính góc giữa hai đường thẳng ∆1 và ∆2 trong các trường hợp sau: Δ1: y = –2x + 4 và Δ2: y = x 2 + 3 2
Cách 1:
Δ1: y = –2x + 4 ⇔ 2x + y – 4 = 0
Δ2: 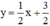 ⇔ x - 2y + 3 = 0
⇔ x - 2y + 3 = 0
Hai đường thẳng Δ1 và Δ2 có vecto pháp tuyến lần lượt là: n1→(2;1); n2→(1;-2)
Góc giữa (Δ1) và (Δ2):
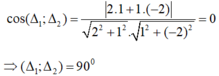
Cách 2:
Δ1: y = –2x + 4 có hệ số góc k1 = –2
Δ2: 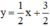 có hệ số góc k2 = 1/2
có hệ số góc k2 = 1/2
Nhận thấy k1.k2 = –1 nên Δ1 ⊥ Δ2 ⇒ (Δ1, Δ2) = 90°.
Đúng 0
Bình luận (0)


