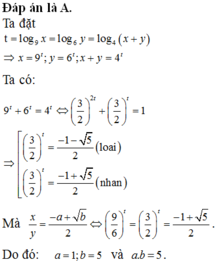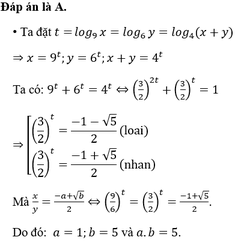cho hai số nguyên x,y thỏa mãn các điều kiện sau : xy=1261; x - y chia hết cho -84 và x<0. khi đó x,y là ?
KH
Những câu hỏi liên quan
Cho hai số nguyên x;y thỏa mãn các điều kiện sau xy=1261; x - y = -84 và x < 0.x;y là bao nhiêu?
Ai giải đúng và nhanh nhất mình cho 3 like
Ta có x-y= - 84=> y=84+x
Nên xy=1261
=> x(x+84)=1261
=> x2+84x-1261=0
=> x2+97x-13x-1261=0
=> x(x+97)-13(x+97)=0
=> (x-13)(x+97)=0
=> x-13=0=> x=13
x+97=0=> x=-97
+) trường hợp 1 với x=13, có
x-y=-84
=> -13-y=-84
=>y=71
Vậy với x=13 thì y= 71
=) trường hợp 2 với x=-97,có
x-y=-84
-97-y=-84
y=-13
Vậy với x=-97 thì y=-13
Đúng 0
Bình luận (0)
tìm các số nguyên x,y thỏa mãn cả hai điều kiện x.y =1261 và x-y=-84
Tìm các số nguyên x,y thỏa mãn cả 2 điều kiện :
x.y=1261
x-y=-84
Lời giải:
Do x − y = −84 nên x < y hơn nữa x, y cùng tính chẵn lẻ.
Lại có 1261 = 1.1261 = 13.97 = (−1).(−1261) = (−13).(−97)
Ta có bảng sau:
Vậy x = 13; y = 97 hoặc x = −97; y = −13
Đơn giản hóa x + -1y = 84 Giải quyết x + -1y = 84 Giải quyết cho biến 'x'. Di chuyển tất cả các cụm từ có chứa x sang trái, tất cả các thuật ngữ khác ở bên phải. Thêm 'y' vào mỗi bên của phương trình. x + -1y + y = 84 + y Kết hợp như các thuật ngữ: -1y + y = 0 x + 0 = 84 + y x = 84 + y Đơn giản hóa x = 84 + y
Đúng 0
Bình luận (0)
Tìm các số nguyên x,y thỏa mãn:
a) x. y = 1261 và x - y = 84
b) (y+1).(xy - 1) = 3
a/
$x-y=84\Rightarrow x=84+y$. Thay vào điều kiện đầu tiên thì:
$(84+y)y=1261$
$\Rightarrow y^2+84y-1261=0$
$\Rightarrow (y-13)(y+97)=0$
$\Rightarrow y-13=0$ hoặc $y+97=0$
$\Rightarrow y=13$ hoặc $y=-97$
Nếu $y=13$ thì $x=84+y=84+13=97$
Nếu $y=-97$ thì $x=84+(-97)=-13$
Đúng 0
Bình luận (0)
b/
Do $x,y$ nguyên nên $xy-1, y+1$ cũng là số nguyên. Mà tích của chúng bằng $3$ nên ta có các TH sau:
TH1: $y+1=1, xy-1=3\Rightarrow y=0; xy=4$ (vô lý, vì 0 nhân với số nào cũng bằng 0)
TH2: $y+1=-1, xy-1=-3\Rightarrow y=-2; xy=-2\Rightarrow x=1$
TH3: $y+1=3, xy-1=1\Rightarrow y=2; xy=2\Rightarrow x=1$
TH4: $y+1=-3, xy-1=-1\Rightarrow y=-4; xy=0$ (vô lý do $0$ nhân với số nào cũng bằng $0$)
Vậy.........
Đúng 0
Bình luận (0)
Tìm các số nguyên x,y thỏa mãn điều kiện : x-2y=3-xy
Gọi x, y là các số thực dương thỏa mãn điều kiện
log
9
x
log
6
y
log
4
(
x
+
y
)
và
x
y
-
a
+
b
2
, với a, b là hai số nguyên dương. Tính a.b.
Đọc tiếp
Gọi x, y là các số thực dương thỏa mãn điều kiện log 9 x = log 6 y = log 4 ( x + y ) và x y = - a + b 2 , với a, b là hai số nguyên dương. Tính a.b.
![]()
![]()
![]()
![]()
Gọi x,y là các số thực dương thỏa mãn điều kiện
l
o
g
9
x
l
o
g
6
y
l
o
g
4
(
x
+
y
)
và
x
y
-
a
+
b
2...
Đọc tiếp
Gọi x,y là các số thực dương thỏa mãn điều kiện l o g 9 x = l o g 6 y = l o g 4 ( x + y ) và x y = - a + b 2 , với a,b là hai số nguyên dương. Tính a.b
A. a.b=5
B. a.b=1
C. a.b=8
D. a.b=4
Tìm tất cả các số nguyên x;y thỏa mãn điều kiện
xy-2x+3x=5
B1 cho các số nguyên a,b,c,d thỏa mãn đồng thời 2 điều kiện sau a+b+cd+1 và a^2+b^2+c^2d^2+2d-1 chứng minh rằng (a^2+1)(b^2+1)(c^2+1) là số chính phươngB2 cho biểu thức Afrac{x^2}{y^2+xy}-frac{y^2}{x^2-xy}-frac{x^2+y^2}{xy}(xyne0,yne+-x)A) rút gọn Ab)tính giá trị của A^2 biết x,y thỏa mãn điều kiện x^2+y^23xyc) chứng minh rằng biểu thức A không nhân giá trị nguyên với mọi giá trị nguyên của x,y thỏa mãn điều kiện ở trênB3 tìm các cặp số (x;y) thỏa mãn điều kiện 4x^2+2y^2-4xy-16x-2y+410
Đọc tiếp
B1 cho các số nguyên a,b,c,d thỏa mãn đồng thời 2 điều kiện sau a+b+c=d+1 và a^2+b^2+c^2=d^2+2d-1 chứng minh rằng (a^2+1)(b^2+1)(c^2+1) là số chính phương
B2 cho biểu thức A=\(\frac{x^2}{y^2+xy}\)-\(\frac{y^2}{x^2-xy}\)-\(\frac{x^2+y^2}{xy}\)(xy\(\ne\)0,y\(\ne\)+-x)
A) rút gọn A
b)tính giá trị của A^2 biết x,y thỏa mãn điều kiện x^2+y^2=3xy
c) chứng minh rằng biểu thức A không nhân giá trị nguyên với mọi giá trị nguyên của x,y thỏa mãn điều kiện ở trên
B3 tìm các cặp số (x;y) thỏa mãn điều kiện 4x^2+2y^2-4xy-16x-2y+41=0