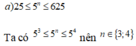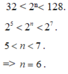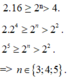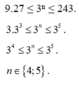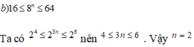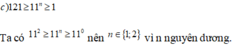Tìm số nguyên dương n biết: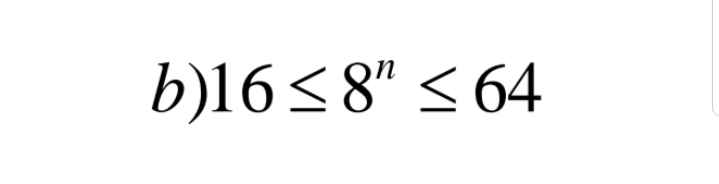
LO
Những câu hỏi liên quan
Gọi S(n) là tổng tất cả các chữ số của số nguyên dương n khi biểu diễn nó trong hệ thập phân. Biết rằng với mọi số nguyên dương n thì ta có 0<S(n)<=n. Tìm số nguyên dương n sao cho S(n)=n^2- 2011n+ 2010
\(^∗\)Xét \(n=2011\)thì \(S\left(2011\right)=2011^2-2011.2011+2010=2010\)(vô lí)
\(^∗\)Xét \(n>2011\)thì \(n-2011>0\)do đó \(S\left(n\right)=n\left(n-2011\right)+2010>n\left(n-2011\right)>n\)(vô lí do \(S\left(n\right)\le n\))
* Xét \(1\le n\le2010\)thì \(\left(n-1\right)\left(n-2010\right)\le0\Leftrightarrow n^2-2011n+2010\le0\)hay \(S\left(n\right)\le0\)(vô lí do \(S\left(n\right)>0\))
Vậy không tồn tại số nguyên dương n thỏa mãn đề bài
Tìm số nguyên dương n biết: 25 ≤ 5 n ≤ 625
Tìm số nguyên dương n, biết:16 ≤ 8n ≤ 64.
Từ đề bài suy ra 24 ≤ 23n ≤ 26, tìm được n = 2
Đúng 0
Bình luận (0)
Tìm số nguyên dương n biết: 32 < 2n< 128
Tìm số nguyên dương n biết: 2.16 ≥ 2n> 4
Tìm số nguyên dương n biết:9.27 ≤ 3n ≤ 243
Tìm số nguyên dương n, biết: 3.27 > 3n ≥ 9
Từ đề bài suy ra 34 > 3n ≥ 32, tìm được n ∈ {2; 3}
Đúng 0
Bình luận (0)
Tìm số nguyên dương n biết: 16 ≤ 8 n ≤ 64
Tìm số nguyên dương n, biết: 25< 5n < 625;
Từ đề bài suy ra 52 < 5n < 54, tìm được n = 3
Đúng 0
Bình luận (0)
Tìm số nguyên dương n biết: 121 ≥ 11 n ≥ 1