Gọi S là diện tích tứ giác ABCD có độ dài các cạnh là a ; b ; c ; d .
CM \(S\le\frac{a^2+b^2+c^2+d^2}{4}\)
gọi S là diện tích tứ giác ABCD có độ dài các cạnh là a,b,c,d .
Chứng minh rằng : S ≤( a2+b2+c2+d2 )/4
Gọi S là diện tích của tứ giác ABCD có độ dài các cạnh là a,b,c,d. CMR: \(S\le\frac{a^2+b^2+c^2+d^2}{2}\)
Vẽ AH _|_ CD: \(S_{ACD}=\frac{1}{2}ah\le\frac{1}{2}ab\)
\(\Rightarrow4S_{ACD}\le2ab\le a^2+b^2\) (Theo BĐT Cosi)
Tương tự \(4S_{ABC}\le c^2+d^2\)
Vậy \(4\left(S_{ACD}+S_{ABC}\right)\le a^2+b^2+c^2+d^2\) hay \(S\le\frac{a^2+b^2+c^2+d^2}{4}\)
Dấu "=" xảy ra <=> \(\Delta\)ABC vuông ở B và \(\Delta\)ADC vuông ở D
=> ABCD là hình vuông
Gọi S là diện tích tứ giác ABCD có độ dài các cạnh là a,c,c,d. CMR: \(S\le\frac{a^2+b^2+c^2+d^2}{4}\)
theo công thức Brahmagupta bđt \(\Leftrightarrow\)\(\sqrt{\frac{\left(a^2+b^2+c^2+d^2\right)^2-2\left(a^4+b^4+c^4+d^4\right)+8abcd}{16}-\frac{1}{4}\left(ac+bd\right)^2+\frac{1}{4}u^2v^2}\le\frac{a^2+b^2+c^2+d^2}{4}\)
Gọi u, v là 2 đường chéo của tứ giác, theo bđt Ptolemy ta coa: \(uv\le ac+bd\)\(\Leftrightarrow\)\(\frac{1}{4}u^2v^2\le\frac{1}{4}\left(ac+bd\right)^2\)
Do đó cần CM: \(\sqrt{\left(a^2+b^2+c^2+d^2\right)^2-2\left(a^4+b^4+c^4+d^4\right)+8abcd}\le a^2+b^2+c^2+d^2\)
\(\Leftrightarrow\)\(\left(a^2+b^2+c^2+d^2\right)^2-2\left(a^4+b^4+c^4+d^4\right)+8abcd\le\left(a^2+b^2+c^2+d^2\right)^2\)
\(\Leftrightarrow\)\(a^4+b^4+c^4+d^4\ge4abcd\) ( đúng theo Cosi )
Dấu "=" xảy ra khi ABCD là hình vuông
Cho tứ diện đều ABCD có độ dài các cạnh bằng 2a . Gọi M , N lần lượt là trung điểm các cạnh AC , BC ; P là trọng tâm tam giác BCD . Mặt phẳng (MNP) cắt tứ diện theo một thiết diện có diện tích là:
A. a 2 11 2
B. a 2 2 4
C. a 2 11 4
D. a 2 3 4
Cho tứ diện đều ABCD có độ dài các cạnh bằng 2a . Gọi M , N lần lượt là trung điểm các cạnh AC , BC ; P là trọng tâm tam giác BCD . Mặt phẳng (MNP) cắt tứ diện theo một thiết diện có diện tích là:
A . a 2 11 2
B . a 2 2 4
C . a 2 11 4
D . a 2 3 4
Đáp án D
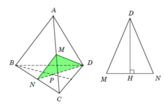
Trong tam giác BCD có: P là trọng tâm, N là trung điểm BC . Suy ra N , P , D thẳng hàng.
Vậy thiết diện là tam giác MND .
Xét tam giác MND , ta có ![]()
![]()
Do đó tam giác MND cân tại D .
Gọi H là trung điểm MN suy ra DH ⊥ MN
Diện tích tam giác ![]()
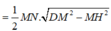
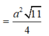
Cho S là diện tích của tứ giác ABCD có độ dài các cạnh là a, b, c, d. Chứng minh S ≤ (a^2 + b^2 + c^2 + d^2)/4
Cho tứ diện đều ABCD có độ dài các cạnh bằng 2a. Gọi M và N lần lượt là trung điểm của AC và BC; P là trọng tâm tam giác BCD. Mặt phẳng (MNP) cắt tứ diện theo 1 thiết diện có diện tích là
A. a 2 11 2 .
B. a 2 2 4 .
C. a 2 11 4 .
D. a 2 3 4 .
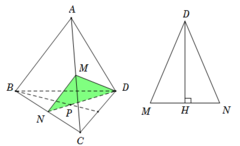
Trong tam giác BCD có: Plà trọng tâm, N là trung điểm BC .
Suy ra N; P; D thẳng hàng.
Vậy thiết diện là tam giác MND..
Xét tam giác MND, ta có M N = A B 2 = a ; D M = D N = A D 3 2 = a 3
Do đó tam giác MND cân tại D.
Gọi H là trung điểm MN suy ra DH và MN vuông góc với nhau..
Diện tích tam giác S Δ M N D = 1 2 M N . D H = 1 2 M N . D M 2 − M H 2 = a 2 11 4
Chọn C.
Cho tứ diện ABCD có AB = x, tất cả các cạnh còn lại có độ dài bằng 2. Gọi S là diện tích tam giác ABC, h là khoảng cách từ D đến mp(ABC).Với giá trị nào của x thì biểu thức V = 1 3 S . h đạt giá trị lớn nhất.
A. x = 1
B. x = 6
C. x = 2 6
D. x = 2
Đáp án B
Gọi K là trung điểm của AB, do ∆CAB và ∆DAB là hai tam giác cân chung cạnh đáy AB nên C K ⊥ A B D K ⊥ A B ⇒ A B ⊥ C D K
Kẻ D H ⊥ C K ta có D H ⊥ A B C
Vậy V = 1 3 S . h = 1 3 1 2 C K . A B . D H = 1 3 1 2 C K . D H . A B
Suy ra V = 1 3 A B . S Δ K D C
Dễ thấy Δ C A B = Δ D A B ⇒ C K = D K h a y Δ K D C cân tại K. Gọi I là trung điểm CD, suy ra K I ⊥ C D và K I = K C 2 − C I 2 = A C 2 − A K 2 − C I 2 = 4 − x 2 4 − 1 = 1 2 12 − x 2
Suy ra S Δ K D C = 1 2 K I . C D = 1 2 12 − x 2
Vậy V = 1 6 x 12 − x 2 ≤ 1 6 . x 2 + 12 − x 2 2 = 1 . Dấu đẳng thức xảy ra khi và chỉ khi x = 12 − x 2 h a y x = 6
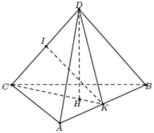
Cho tứ diện ABCD có AB = x, tất cả các cạnh còn lại có độ dài bằng 2. Gọi S là diện tích tam giác ABC, h là khoảng cách từ D đến mp (ABC).Với giá trị nào của x thì biểu thức V = 1 3 S h đạt giá trị lớn nhất.
A. x = 1
B. x = 6
C. x = 2 6
D. x = 2