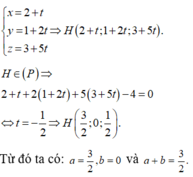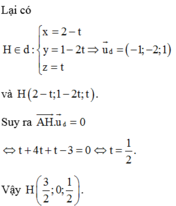Cho d: x-my-2m+3=0 và điểm A (1;1) và điểm B (2;5) a) tìm m để 2 điểm A và B nằm cùng về 1 phía với đường thẳng d b) tìm m để 2 điểm A và B nằm khác phía với d
NT
Những câu hỏi liên quan
Định m để:
a) Hai đường thẳng (d): y=2x-1 +2m và (d'): y=-x-2m cắt nhau tại 1 điểm có hoành độ dương
b) Hai đường thẳng (D1): mx+y=2m và (D2): (2m+1)x+my=2m^2 + m -1 cắt nhau tại 1 điểm trên trục tung. Tìm điểm đó
Trong không gian với hệ tọa độ Oxyz cho điểm A (2; 1; 3) và mặt phẳng (P): x + my + (2m + 1)z – m – 2 0, m là tham số. Gọi H (a; b; c) là hình chiếu vuông góc của điểm A trên (P). Tính a + b khi khoảng cách từ điểm A đến (P) lớn nhất? A. a + b -1/2 B. a + b 2 C. a + b 0 D. a + b 3/2
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho điểm A (2; 1; 3) và mặt phẳng (P): x + my + (2m + 1)z – m – 2 = 0, m là tham số. Gọi H (a; b; c) là hình chiếu vuông góc của điểm A trên (P). Tính a + b khi khoảng cách từ điểm A đến (P) lớn nhất?
A. a + b = -1/2
B. a + b = 2
C. a + b = 0
D. a + b = 3/2
Chọn D
Ta có x + my + (2m + 1)z – m – 2 = 0 <=> m(y + 2z -1) + x + z - 2 = 0 (*)
Phương trình (*) có nghiệm với 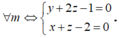
Suy ra (P) luôn đi qua đường thẳng 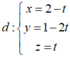
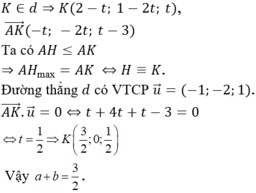
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho điểm A(2;1;3) và mặt phẳng (P): x + my + (2m + 1) - m - 2 = 0. Gọi H (a;b;c) là hình chiếu vuông góc của điểm A trên (P) Khi khoảng cách từ điểm A đến (P) lớn nhất, tính a + b
A. 2
B. 1
C. 3 2
D. 0
Cho hàm số y = f(x) = mx + 2m − 3 có đồ thị (d). gọi A, B là hai điểm thuộc đồ thị
và có hoành độ lần lượt là −1 và 2.
1 Xác định tọa độ hai điểm A và B.
2 Tìm m để cả hai điểm A và B cùng nằm phía trên trục hoành.
3 Tìm điều kiện của m để f(x) > 0, ∀x ∈ [−1; 2]
Cho hai đường thẳng (d1 ) : y = (m +1)x + m+3 và (d2 ) : y= (2m+1)x-m+3 với m khác 0. Tìm tất cả các giá trị m (m khác 0) để (d1) và (d1) cắt nhau tại điểm M sao cho M nằm trên đường thẳng (d): y=x
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;3) và mặt phẳng
P
:
x
+
m
y
+
(
2
m
+
1
)
z
-
(
2
+
m
)
0
với m là tham số. Gọi điểm H(a;b;c) là hình chiếu vuông góc của điểm A trên (P). Tính a+b khi khoảng cách từ điểm A đến (P) lớn n...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;3) và mặt phẳng P : x + m y + ( 2 m + 1 ) z - ( 2 + m ) = 0 với m là tham số. Gọi điểm H(a;b;c) là hình chiếu vuông góc của điểm A trên (P). Tính a+b khi khoảng cách từ điểm A đến (P) lớn nhất.
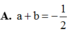
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oyz cho điểm A (2;1;3) và mặt phẳng (P): x+my+ (2m+1)z-m-20, m là tham số. Gọi H (a;b;c) là hình chiếu vuông góc của điểm A trên (P). Tính a+b khi khoảng cách từ điểm A đến (P) lớn nhất? A.
a
+
b
-
1
2
B. a+b2 C. a+b0 D.
a
+
b
3
2
Đọc tiếp
Trong không gian với hệ tọa độ Oyz cho điểm A (2;1;3) và mặt phẳng (P): x+my+ (2m+1)z-m-2=0, m là tham số. Gọi H (a;b;c) là hình chiếu vuông góc của điểm A trên (P). Tính a+b khi khoảng cách từ điểm A đến (P) lớn nhất?
A. a + b = - 1 2
B. a+b=2
C. a+b=0
D. a + b = 3 2
Chọn D
Ta có x + my + (2m + 1)z – m – 2 = 0 ó m(y + 2z – 1) + x + z – 2 = 0 (*)
Phương trình (*) có nghiệm với 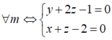
Suy ra (P) luôn đi qua đường thẳng 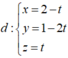
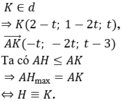
Đường thẳng d có VTCP ![]()
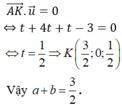
Đúng 0
Bình luận (0)
Câu 1 : Cho hàm số yfrac{x2}{4}và các điểm A ( 1;0.25) ; B (2;2) ; C (4;4) . Các điểm thuộc đồ thị hàm số gồm A )Chỉ có AB) Hai điểm A và CC) Hai điểm A và BD)Cả 3 điểm A,B,CCâu 2 : Điểm M (-1;2) thuộc đồ thị hàm số yax^2khi a A )2B)-2C)4D)-4Câu 3 : Phương trình ( m+1)x^2-2mx+10 là phương trình bậc hai khi :A) mne1B) m0C) mne-1D) mọi giá trị của mCâu 4 : Hệ số b của phương trình x^2-2left(2m-1right)x+2m0 làA) 2m-1B) 2mC) -2(2m-1)D)2(2m-1)Câu 5 : Giải phương trình 0.5x^2+0.15x0Câu 6 Giải phương t...
Đọc tiếp
Câu 1 : Cho hàm số y=\(\frac{x2}{4}\)và các điểm A ( 1;0.25) ; B (2;2) ; C (4;4) . Các điểm thuộc đồ thị hàm số gồm
A )Chỉ có A
B) Hai điểm A và C
C) Hai điểm A và B
D)Cả 3 điểm A,B,C
Câu 2 : Điểm M (-1;2) thuộc đồ thị hàm số y=\(ax^2\)khi a=
A )=2
B)=-2
C)=4
D)=-4
Câu 3 : Phương trình ( m+1)\(x^2\)-2mx+1=0 là phương trình bậc hai khi :
A) m\(\ne\)1
B) m=0
C) m\(\ne\)-1
D) mọi giá trị của m
Câu 4 : Hệ số b của phương trình \(x^2-2\left(2m-1\right)x+2m=0\) là
A) 2m-1
B) 2m
C) -2(2m-1)
D)2(2m-1)
Câu 5 : Giải phương trình \(0.5x^2+0.15x=0\)
Câu 6 Giải phương trình \(\sqrt{5}x^2+\sqrt{15}=0\)
Câu 7 Tìm giá trị nhỏ nhất của hàm số \(y=\left(m^2+1\right)x^2\)
( d ) y = ( m\(^2\) + 2m )x + m + 1 với m là tham số. Tìm điều kiện của m :
a) (d ) song song với đường thẳng d1: y= -x - 2023
b) (d) đi qua điểm A ( 0 ; 2024 )
c) (d) đi qua điểm của 2 đường thẳng ( d2) y= x - 2 và ( d3 ) y= -4x + 3
a: Để (d)//(d1) thì \(\left\{{}\begin{matrix}m^2+2m=-1\\m+1\ne-2023\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2+2m+1=0\\m\ne-2024\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(m+1\right)^2=0\\m\ne-2024\end{matrix}\right.\)
=>(m+1)2=0
=>m+1=0
=>m=-1
b: Thay x=0 và y=2024 vào (d), ta được:
\(0\left(m^2+2m\right)+m+1=2024\)
=>m+1=2024
=>m=2023
c: Tọa độ giao điểm của (d2) và (d3) là:
\(\left\{{}\begin{matrix}x-2=-4x+3\\y=x-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=5\\y=x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1-2=-1\end{matrix}\right.\)
Thay x=1 và y=-1 vào (d), ta được:
\(1\left(m^2+2m\right)+m+1=-1\)
=>\(m^2+3m+2=0\)
=>(m+2)(m+1)=0
=>\(\left[{}\begin{matrix}m+2=0\\m+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-2\\m=-1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho phương trình : x^3 - (m+1) x^2 - (2m^2-3m+2)x + 2m (2m-1) =0. Tìm m để đồ thị giao với trục Ox tại 3 điểm, 2 điểm, 1 điểm.