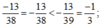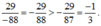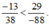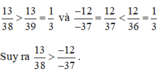so sánh 2^2007 và 3^1338
PA
Những câu hỏi liên quan
So sánh : 31338 và 22007
\(3^{1388}\)=\(3^{2^{669}}\)=\(9^{669}\)
\(2^{2007}\)=\(2^{3^{699}}\)=\(8^{669}\)
Do \(9^{669}\)>\(8^{669}\)=> \(3^{1388}\)>\(2^{2007}\)
Đúng 0
Bình luận (0)
So sánh: 22007 và 31338
xét 22007= (23)669= 8669
xét 31338= (32)669= 9669
mà 8669< 9669
Vậy 22007 < 31338
chắc chắn 100% lun
tk nha
Đúng 0
Bình luận (0)
Cho a, b thỏa mãn a^ 669 + b^ 669 = 30 và a ^ 1338 + b ^ 1338 = 468 Tính H = a^ 2007 + b^2007
So sánh các số hữu tỉ sau bằng cách nhanh nhất: - 13 38 v à 29 - 88
Dựa vào tính chất "Nếu x < y và y < z thì x < z" hãy so sánh: 13 38 v à - 12 - 37
13/38 > -12/-37
chúc bạn học tốt nha
Cho a,b thỏa mãn a669+b669=30 va a1338+b1338=468 .Tinh H=a2007+b2007
Tìm tất cả các số nguyên ( x ; y ) thỏa mãn:
\(x^{2007}=y^{2007}-y^{1338}-y^{669}+2\)
Đặt \(u=x^{669}\); \(v=y^{669}\left(u,v\in Z\right)\)thì PT ( 1 ) có dạng \(u^3=v^3-v^2-v+2\).
Nhận thấy:
\(u^3=v^3-v^2-v+2=\left(v-1\right)^3+2\left(v-1\right)^2+1>\left(v-1\right)^3\)và \(u^3=v^3-\left(v-1\right).\left(v+2\right)\)
+ Nếu \(v>1\)hoặc \(v< -2\)thì \(\left(v-1\right)\left(v+2\right)>0\), suy ra: \(\left(v-1\right)^3< u^3< v^3\Leftrightarrow v-1< u< v\), điều này không thể xảy ra khi \(u,v\in Z.\)
+ Với \(-2\le v\le1\)và \(v\in Z\)thì \(v\in\left\{-2;-1;0;1\right\}\)
Nếu \(v=-2\)thì \(y^{669}=-2\), nên \(y\notin Z.\)
Nếu \(v=-1\)thì \(u=1\), suy ra: \(x=-1;y=1\)
Nếu \(v=0\)thì \(u=2\), suy ra: \(x^{669}=2\), nên \(x\notin Z.\)
Nếu \(v=1\)thì \(u=1\), suy ra: \(x=y=1.\)
Vậy các cặp số nguyên ( x ; y ) thỏa mãn ( 1 ) là ( 1 ; 1 ) và ( 1 ; -1 ).
Đúng 0
Bình luận (0)
So sánh S=√(1*2007)+√(3*2005)+...+√(2007*1) và 1004^2
so sánh 2^2008-3 /2^2007-1 và 2^2007-3 /2^2006-1
Mọi người giúp mik với ạ !!!!!!!!!!!!
\(A=\dfrac{2^{2008}-3}{2^{2007}-1};B=\dfrac{2^{2007}-3}{2^{2006}-1}\)
\(\dfrac{1}{2}A=\dfrac{2^{2008}-3}{2^{2008}-2}=1-\dfrac{1}{2^{2008}-2};\dfrac{1}{2}B=\dfrac{2^{2007}-3}{2^{2007}-2}=1-\dfrac{1}{2^{2007}-2}\)
2^2008-2>2^2007-2
=>1/2^2008-2<1/2^2007-2
=>A>B
Đúng 0
Bình luận (0)