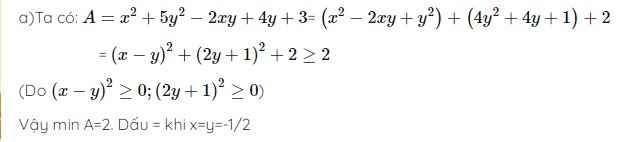a) \(2x^2-x+1=2\left(x-\dfrac{1}{4}\right)^2+\dfrac{7}{8}\ge\dfrac{7}{8}\)

\(ĐTXR\Leftrightarrow x=\dfrac{1}{4}\)

b) \(5x-x^2+4=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{41}{4}\le\dfrac{41}{4}\)

\(ĐTXR\Leftrightarrow x=\dfrac{5}{2}\)

c) \(x^2+5y^2-2xy+4y+3=\left(x-y\right)^2+\left(2y+1\right)^2+2\ge2\)

\(ĐTXR\Leftrightarrow\)\(x=y=-\dfrac{1}{2}\)

b: ta có: \(-x^2+5x+4\)

\(=-\left(x^2-5x-4\right)\)

\(=-\left(x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}-\dfrac{41}{4}\right)\)

\(=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{41}{4}\le\dfrac{41}{4}\forall x\)

Dấu '=' xảy ra khi \(x=\dfrac{5}{2}\)

a: Ta có: \(A=x^2+3x+4\)

\(=x^2+2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}\)

\(=\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\forall x\)

Dấu '=' xảy ra khi \(x=-\dfrac{3}{2}\)

ta có Q= x²-5x= x²-2x\(\frac{5}{2}\)+ \(\frac{25}{4}\)- \(\frac{25}{4}\)= (x-\(\frac{5}{2}\))²-\(\frac{25}{4}\)

vì (x-\(\frac{5}{2}\)) ²>=0

=> Q >= \(\frac{-25}{4}\)

dấu '=' sảy ra khi (x-\(\frac{5}{2}\))²=0

=> x-\(\frac{5}{2}\)=0

=>x=\(\frac{5}{2}\)

vậy Q_(min)=\(\frac{-25}{4}\) khi x= \(\frac{5}{2}\)

Ta có :

\(Q=x^2+5x\)

\(\Rightarrow Q=x^2+2.x.\frac{5}{2}+\frac{25}{4}-\frac{25}{4}\)

\(\Rightarrow Q=\left(x+\frac{5}{2}\right)^2-\frac{25}{4}\)

Vì \(\left(x+\frac{5}{2}\right)^2\ge0\forall x\)

\(\Rightarrow\left(x+\frac{5}{2}\right)^2-\frac{25}{4}\ge-\frac{25}{4}\)

Dấu " = " xảy ra khi x = - 5 / 4

Vậy ......

\(Q=x^2-5x=x^2-2.x.\frac{5}{2}+\frac{25}{4}-\frac{25}{4}\)

\(\Leftrightarrow Q=\left(x-\frac{5}{2}\right)^2-\frac{25}{4}\)

Vì \(\left(x-\frac{5}{2}\right)^2\ge O\Rightarrow Q\ge-\frac{25}{4}\)

Dấu ''='' xảy ra khi \(\left(x-\frac{5}{2}\right)^2=0\Leftrightarrow x=\frac{5}{2}\)

Vậy GTNN của Q = \(\frac{-25}{4}\Leftrightarrow x=\frac{5}{2}\)

a: Ta có: \(A=x^2+2x+5\)

\(=x^2+2x+1+4\)

\(=\left(x+1\right)^2+4\ge4\forall x\)

Dấu '=' xảy ra khi x=-1

\(x^2+x+\frac{1}{x^2}+2x+2=\left(x^2+2+\frac{1}{x^2}\right)+\left(x+1\right)^2-1=\left(x+\frac{1}{x}\right)^2+\left(x+1\right)^2-1\ge-1\)

Vậy giá trị nhỏ nhất của biểu thức trên là -1 khi x=-1.

Áp dụng Bunyakovsky, ta có :

\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)

=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)

=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)

Mấy cái kia tương tự 

1:

a: =x^2-7x+49/4-5/4

=(x-7/2)^2-5/4>=-5/4

Dấu = xảy ra khi x=7/2

b: =x^2+x+1/4-13/4

=(x+1/2)^2-13/4>=-13/4

Dấu = xảy ra khi x=-1/2

e: =x^2-x+1/4+3/4=(x-1/2)^2+3/4>=3/4

Dấu = xảy ra khi x=1/2

f: x^2-4x+7

=x^2-4x+4+3

=(x-2)^2+3>=3

Dấu = xảy ra khi x=2

2:

a: A=2x^2+4x+9

=2x^2+4x+2+7

=2(x^2+2x+1)+7

=2(x+1)^2+7>=7

Dấu = xảy ra khi x=-1

b: x^2+2x+4

=x^2+2x+1+3

=(x+1)^2+3>=3

Dấu = xảy ra khi x=-1