Dựng tam giác abc vuông tại a biết cạnh huyền bc=5cm góc nhọn b=70 độ
mong mng giúp em ạ,em cảm ơn
Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4cm, góc nhọn B = 65o.
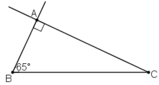
a) Phân tích
Giả sử dựng được ΔABC thỏa mãn yêu cầu đề bài.
Đoạn thẳng BC dựng được vì đã biết độ dài.
Khi đó điểm A là giao điểm của:
+ Tia Bx tạo với đoạn thẳng BC góc 65º
+ Đường thẳng qua C và vuông góc với tia Bx vừa dựng.
b) Cách dựng:
- Dựng đoạn thẳng BC = 4cm.
- Dựng tia Bx tạo với BC một góc 65º.
- Dựng đường thẳng a qua C và vuông góc với Bx.
- Bx cắt a tại A.
ΔABC là tam giác cần dựng.
c) Chứng minh: ΔABC vừa dựng vuông tại A, góc B = 65º và BC = 4cm.
d) Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện đề bài.
Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4cm, góc nhọn B = 65o.
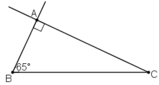
a) Phân tích
Giả sử dựng được ΔABC thỏa mãn yêu cầu đề bài.
Đoạn thẳng BC dựng được vì đã biết độ dài.
Khi đó điểm A là giao điểm của:
+ Tia Bx tạo với đoạn thẳng BC góc 65º
+ Đường thẳng qua C và vuông góc với tia Bx vừa dựng.
b) Cách dựng:
- Dựng đoạn thẳng BC = 4cm.
- Dựng tia Bx tạo với BC một góc 65º.
- Dựng đường thẳng a qua C và vuông góc với Bx.
- Bx cắt a tại A.
ΔABC là tam giác cần dựng.
c) Chứng minh: ΔABC vừa dựng vuông tại A, góc B = 65º và BC = 4cm.
d) Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện đề bài.
Tam giác ABC vuông tại A có AB=3cm, BC=5cm. Độ dài cạnh AC bằng bao nhiêu?
em đg cần gấp ạaaaa cảm ơn mng><
Áp dung định lí Pytago ta có
AB2 + AC2 = BC2
hay 32 + AC2 = 52
AC2 = 52-32
AC2 = 252-92
AC2 = \(\sqrt{16}\)
AC= 4cm
Áp dung định lí Pytago ta có
AB2 + AC2 = BC2
hay 32 + AC2 = 52
AC2 = 52-32
AC2 = 25-9
AC = √16
AC= 4cm
Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 5cm, B = 35 0
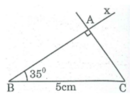
Cách dựng:
- Dựng đoạn BC = 5cm
- Dựng góc ∠ CBx = 35 0
- Dựng CA ⊥ Bx ta có ∆ ABC dựng được.
Chứng minh: ∆ ABC có ∠ A = 90o, ∠ B = 35 0 , BC = 5cm. Thỏa mãn điều kiện bài toán.
Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4cm, góc nhọn \(\widehat{B}=65^0\)
Bài giải:
Sử dụng phương pháp dựng tam giác vuông đã được học.
Ta lần lượt thực hiên:
- Vẽ đoạn BC = 4cm.
- Vẽ tia Bx tạo với BC một góc 650
- Vẽ đường thẳng a qua C và vuông góc với Bx và cắt Bx tại A.
Khi đó ∆ABC là tam giác cần dựng.
Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4cm, góc nhọn ˆBB^=650
Bài giải:
Sử dụng phương pháp dựng tam giác vuông đã được học.
Học sinh tự vẽ hình
Ta lần lượt thực hiên:
- Vẽ đoạn BC = 4cm.
- Vẽ tia Bx tạo với BC một góc 650
- Vẽ đường thẳng a qua C và vuông góc với Bx và cắt Bx tại A.
Khi đó ∆ABC là tam giác cần dựng.
Ta lần lượt thực hiên:
– Vẽ đoạn BC = 4cm.
– Vẽ tia Bx tạo với BC một góc 650
– Vẽ đường thẳng a qua C và vuông góc với Bx và cắt Bx tại A.
Khi đó ∆ABC là tam giác cần dựng.
Bài giải:
Sử dụng phương pháp dựng tam giác vuông đã được học.
Học sinh tự vẽ hình
Ta lần lượt thực hiên:
- Vẽ đoạn BC = 4cm.
- Vẽ tia Bx tạo với BC một góc 650
- Vẽ đường thẳng a qua C và vuông góc với Bx và cắt Bx tại A.
Khi đó ∆ABC là tam giác cần dựng.
mọi người giúp em vs ạ ( vẽ hình luôn giúp em ạ )
Cho tam giác ABC vuông tại A với AC<AB
a)Biết AB=12cm,BC=15cm.TÍnh AC
b) Gọi M là trung điểm của cạnh BC.Qua M kẻ đường thẳng d vuông góc với BC, d cắt tia CA tại G và cắt AB tại D.Chứng minh rằng DC=DB và so sánh AD và DB
c) Kẻ DH vuông góc với GB ( H thuộc GB).Chứng minh ba điểm C.D.H thẳng hàng và AH//BC
Em cảm ơn mng ạ
a)Áp dụng Định lý Pythagoras cho tam giác vuông ABC:AB2+AC2=BC2<=>BC2-AB2=AC2=>AC2=152-122=81=>AC=9
b) Xét \(\Delta\)DBM và \(\Delta\)DCM:
DMB=DMC=90
BM=CM( M là trung điểm BC)
DM:chung
=>\(\Delta\)DBM=\(\Delta\)DCM(c-g-c)=>DC=DB
Xét \(\Delta\)ACD:A=90=>DC>DA
Mà DC=DB(chứng minh trên)
Nên:AD<DB
c)Xét \(\Delta\)BCG:BA \(\perp\)CG;GM\(\perp\)BC
Mà BA cắt GM tại D
Nên: D là trực tâm tam giác BCG
Lại có:CH\(\perp\)GB
Suy ra: C;D;H thẳng hàng
c)Xét \(\Delta\)GBC:GM là đường cao đồng thời là đường trung tuyến
=>\(\Delta\)GBC cân tại G=>GM là đường phân giác
Xét \(\Delta\)GDA và \(\Delta\)GDH:
GAD=GHD=90
GD:chung
AGD=HGD
=>\(\Delta\)GAD=\(\Delta\)GDH(cạnh huyền- góc nhọn)
=>AD=HD=>DAH=DHA=(180-HDA)/2
Xét \(\Delta\)DBC:DC=DB(chứng minh trên)=>DCB=DBC=(180-BDC)/2
Do HDA=BDC(đối đỉnh)
Nên AHD=BCD
Mà C;H;D thẳng hàng(chứng minh trên)
Suy ra AH//BC
cảm ơn bạn đã giúp mình
Bạn ơi bạn vẽ lại hình giúp mình được ko ???
1: Cho tam giác ABC vuông tại A có AB = 2AC, cạnh huyền BC = 5.
a) Tính tan B.
b) Tính cạnh AC.
giúp mik vs ạ cảm ơn nhiều.
a) tanB = AC/AB = 1/2
b) ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= (2AC)² + AC²
= 5AC²
⇒ AC² = BC²/5
= 25/5
= 5
⇒ AC = √5
Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4cm, cạnh góc vuông BC = 2cm.
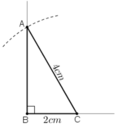
a) Phân tích:
Giả sử dựng được ΔABC thỏa mãn yêu cầu.
Ta dựng được đoạn BC vì biết BC = 2cm.
Khi đó điểm A là giao điểm của:
+ Tia Bx vuông góc với BC
+ Cung tròn tâm C bán kính 4cm.
b) Cách dựng:
+ Dựng đoạn thẳng BC = 2cm.
+ Dựng tia Bx vuông góc với cạnh BC.
+ Dựng cung tròn tâm C, bán kính 4cm. Cung tròn cắt tia Bx tại A.
Kẻ AC ta được ΔABC cần dựng.
c) Chứng minh
ΔABC có góc B = 90º, BC = 2cm.
A thuộc cung tròn tâm C bán kính 4cm nên AC = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.
Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4cm, cạnh góc vuông BC = 2cm.
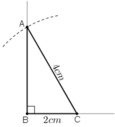
a) Phân tích:
Giả sử dựng được ΔABC thỏa mãn yêu cầu.
Ta dựng được đoạn BC vì biết BC = 2cm.
Khi đó điểm A là giao điểm của:
+ Tia Bx vuông góc với BC
+ Cung tròn tâm C bán kính 4cm.
b) Cách dựng:
+ Dựng đoạn thẳng BC = 2cm.
+ Dựng tia Bx vuông góc với cạnh BC.
+ Dựng cung tròn tâm C, bán kính 4cm. Cung tròn cắt tia Bx tại A.
Kẻ AC ta được ΔABC cần dựng.
c) Chứng minh
ΔABC có góc B = 90º, BC = 2cm.
A thuộc cung tròn tâm C bán kính 4cm nên AC = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.