Giúp mình bài 55 đến 59 với và làm luôn dấu đẳng thức xảy ra

NN
Những câu hỏi liên quan
Mm ơi giúp mình câu 52 đến 54 với nhớ làm dấu đẳng thức xảy ra luôn mình cảm ơn
Giúp mình 3 bài này với với lại làm luôn dấu bằng xảy ra mình cảm ơn
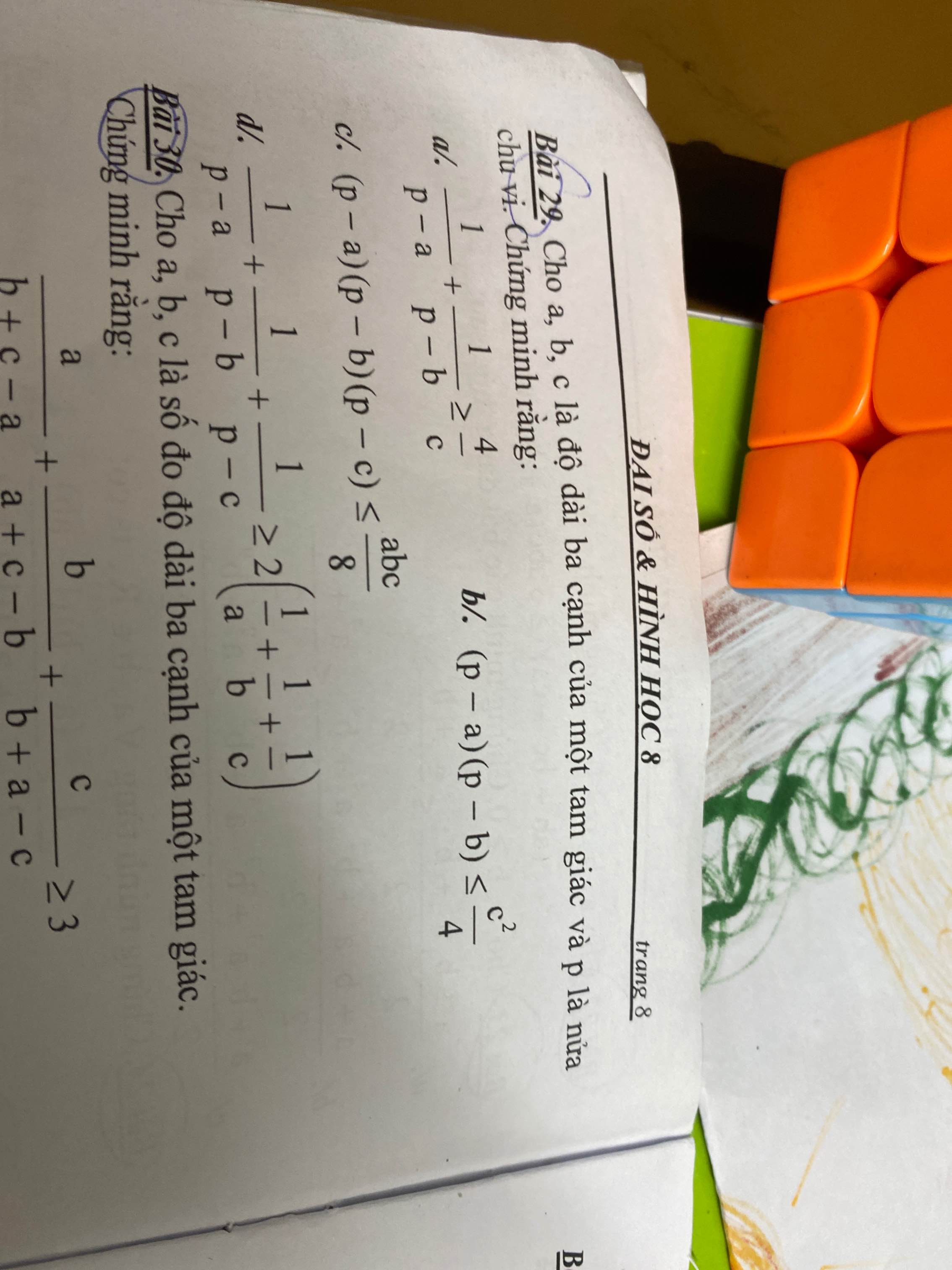
Cho a,b,c thuộc R . CM Bất đẳng thức sau và cho biết dấu = xảy ra khi nào?
h) a 2+4b2+3c2 +14> 2a+12b+6c
Mn làm giúp dùm e bài này với ạ.
Cho a,b,c thuộc R . CM Bất đẳng thức sau và cho biết dấu = xảy ra khi nào?
g) a2+b2+c2-4a-6b-2c+14 ≥0
h) a 2+4b2+3c2 +14> 2a+12b+6c
Mn làm giúp dùm e bài này với ạ.
a: \(\Leftrightarrow a^2-4a+4+b^2-6b+9+c^2-2c+1>=0\)
\(\Leftrightarrow\left(a-2\right)^2+\left(b-3\right)^2+\left(c-1\right)^2>=0\)
Dấu '=' xảy ra (a,b,c)=(2;3;1)
Đúng 1
Bình luận (1)
Bỏ dấu ngoặc rồi tính các tổng sau (từ Bài 3.20 đến Bài 3.21)
3.20.a)(-28)+(-35)-92+(-82)
b)15-(-38)+(-55)-(+47)
3.21.a)(62-81)-(12-59+9)
b)39+(13-26)-(62+39)
giúp mik với làm chi tiết nhé
3.20
a) (-28) + (-35) – 92 + (-82)
= -28 – 35 – 92 – 82
= - (28 + 35 + 92 + 82)
= - [(28 + 82) + (35 + 92)]
= - (110 + 127)
= - 237.
b) 15 – (-38) + (-55) – (+47)
= 15 + 38 – 55 – 47
= 53 – 55 – 47
= - (55 – 53) – 47
= - 2 – 47
= - (2 + 47)
= - 49
Đúng 4
Bình luận (1)
Bài 3.20:
a: =-28-35-92-82
=-110-127
=-237
b: =15+38-55-47
=-40-47+38
=-2-47
=-49
Bài 3.21:
a: =62-81-12+59-9=50+50-81=19
b: =39-13-62-39=-75
Đúng 1
Bình luận (1)
3.21
a) (62 - 81) – (12 – 59 + 9)
= 62 – 81 – 12 + 59 – 9
= (62 – 12) – (81 + 9) + 59
= 50 – 90 + 59
= - (90 – 50) + 59
= - 40 + 59
= 59 – 40
= 19
b) 39 + (13 – 26) – (62 + 39)
= 39 + 13 – 26 – 62 – 39
= (39 – 39) – (26 + 62) + 13
= 0 – 88 + 13
= - 88 + 13
= - (88 – 13)
= - 75.
Đúng 2
Bình luận (1)
Xem thêm câu trả lời
CMR với 2 số thực a,b bất kì ta luôn có \(\left(\frac{a+b}{2}\right)^2\ge ab\)
Dấu đẳng thức xảy ra khi nào?
Ta co \(\left(a-b\right)^2\ge0\)\(\forall_{a,b}\in R\)
=> \(a^2-2ab+b^2\ge0\)
=>\(a^2+2ab+b^2\ge4ab\)
=>\(\left(a+b\right)^2\ge4ab\)
=>\(\left(\frac{a+b}{2}\right)^2\ge ab\)
Đúng 0
Bình luận (0)
chứng minh với mọi số thực t\(\ne0\)
ta luôn có bất đẳng thức sau:
\(t^2+\frac{1}{t^2}+3\ge\frac{5}{2}\left(t+\frac{1}{t}\right)\)
dấu đẳng thức xảy ra khi nào
sử dụng \((t+1/t)^2 = t^2 + 1/t^2 +2\)
Những đẳng thức đáng nhớ
( 4x + 1)^2
( a + 2) ^2
Mình làm bằng hai cách cô dạy nhưng có cách thì ra mũ này, mũ kia. Giúp mình với T.T chỉ mình cách làm luôn nhé
1 Bảy hàng đẳng thức đáng nhớ:
1. (A +B)2 = A2 + 2AB + B2
2. (A - B)2 = A2 - 2AB +B2
3. A2 - B2 = (A - B).(A + B)
4. (A + B)3 = A3 +3A2B +3AB2 +B3
5. (A - B)3 = A3 - 3A2B - 3AB2 -B3
6. A3 + B3 = (A+B).(A2 - AB +B2)
7. A3 - B3 = (A-B) . (A2 + AB + B2)
Chú ý: Các hàng đẳng thức (4) và (5) nhiều khi còn được viết dưới dạng sau:
(A + B)3 = A3 + B3 +3AB.( A + B)
(A - B)3 = A3 - B3 - 3AB.(A - B)
2 Bình phương một tổng N hạng tử:
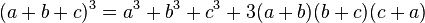

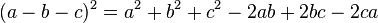

3 Mở rộng( nhị thức newton)
Định lí này nằm trong đặc biệt đã được giảng dạy ở các trung học và mang tên là các Hằng đẳng thức đáng nhớ
Ví dụ: điển hình nhất là nhị thức là công thức bình phương của x + y
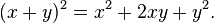
Hệ số nhị thức xuất hiện ở phép triển khai này tương ứng với hàng thứ ba của tam giác Pascal. Các hệ số có lũy thừa cao hơn của x + y tương ứng với các hàng sau của tam giác:
![\begin{align} (x+y)^3 & = x^3 + 3x^2y + 3xy^2 + y^3, \\[8pt] (x+y)^4 & = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4, \\[8pt] (x+y)^5 & = x^5 + 5x^4y + 10x^3y^2 + 10x^2y^3 + 5xy^4 + y^5, \\[8pt] (x+y)^6 & = x^6 + 6x^5y + 15x^4y^2 + 20x^3y^3 + 15x^2y^4 + 6xy^5 + y^6, \\[8pt] (x+y)^7 & = x^7 + 7x^6y + 21x^5y^2 + 35x^4y^3 + 35x^3y^4 + 21x^2y^5 + 7xy^6 + y^7. \end{align}](https://upload.wikimedia.org/math/0/5/9/05912cb66ba1a0cc47688071d5cdae8a.png)
Tam giác Pascal
Chú ý rằng:
lũy thừa của x giảm dần cho tới khi đạt đến 0 (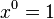 ), giá trị bắt đầu là n (n trong
), giá trị bắt đầu là n (n trong  .)lũy thừa của y tăng lên bắt đầu từ 0 (
.)lũy thừa của y tăng lên bắt đầu từ 0 (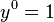 ) cho tới khi đạt đến n (n trong
) cho tới khi đạt đến n (n trong  .)hàng nth của tam giác Pascal sẽ là các hệ số của nhị thức mở rộng (chú ý rằng đỉnh là hàng 0)với mỗi hàng, tích số (tổng của các hệ số) bằng
.)hàng nth của tam giác Pascal sẽ là các hệ số của nhị thức mở rộng (chú ý rằng đỉnh là hàng 0)với mỗi hàng, tích số (tổng của các hệ số) bằng  .với mỗi hàng, nhóm tích số bằng
.với mỗi hàng, nhóm tích số bằng  .
.Định lý nhị thức có thể áp dụng với lũy thừa của bất cứ nhị thức nào. Ví dụ:
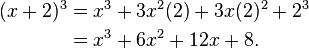
Với một nhị thức có phép trừ, định lý có thể được áp dụng khi sử dụng phép nghịch đảo số hạng thứ hai.
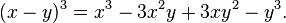
4.Bài tập:
16. Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu;
a) x2 + 2x + 1; b) 9x2 + y2 + 6xy;
c) 25a2 + 4b2 – 20ab; d) x2 – x + .
Bài giải:
a) x2 + 2x + 1 = x2+ 2 . x . 1 + 12
= (x + 1)2
b) 9x2 + y2+ 6xy = (3x)2 + 2 . 3 . x . y + y2 = (3x + y)2
c) 25a2 + 4b2– 20ab = (5a)2 – 2 . 5a . 2b + (2b)2 = (5a – 2b)2
Hoặc 25a2 + 4b2 – 20ab = (2b)2 – 2 . 2b . 5a + (5a)2 = (2b – 5a)2
d) x2 – x + = x2 – 2 . x .
+
=
Hoặc x2 – x + =
- x + x2 =
- 2 .
. x + x2 =
17. Chứng minh rằng:
(10a + 5)2 = 100a . (a + 1) + 25.
Từ đó em hãy nêu cách tính nhẩm bình phương của một số tự nhiên có tận cùng bằng chữ số 5.
Áp dụng để tính: 252, 352, 652, 752.
Bài giải:
Ta có: (10a + 5)2 = (10a)2 + 2 .10a . 5 + 52
= 100a2 + 100a + 25
= 100a(a + 1) + 25.
Cách tính nhaame bình thường của một số tận cùng bằng chữ số 5;
Ta gọi a là số chục của số tự nhiên có tận cùng bằng 5 => số đã cho có dạng 10a + 5 và ta được
(10a + 5)2 = 100a(a + 1) + 25
Vậy để tính bình phương của một số tự nhiên có tận cùng bởi chữ số 5 ta tính tích a(a + 1) rồi viết 25 vào bên phải.
Áp dụng;
- Để tính 252 ta tính 2(2 + 1) = 6 rồi viết tiếp 25 vào bên phải ta được 625.
- Để tính 352 ta tính 3(3 + 1) = 12 rồi viết tiếp 25 vào bên phải ta được 1225.
- 652 = 4225
- 752 = 5625.
18. Hãy tìm cách giúp bạn An khôi phục lại những hằng đẳng thức bị mực làm nhòe đi một số chỗ:
a) x2 + 6xy + … = (… + 3y)2;
b) ... – 10xy + 25y2 = (… - …)2;
Hãy nêu một số đề bài tương tự.
Bài giải:
a) x2 + 2 . x . 3y + … = (…+3y)2
x2 + 2 . x . 3y + (3y)2 = (x + 3y)2
Vậy: x2 + 6xy +9y2 = (x + 3y)2
b) …-2 . x . 5y + (5y)2 = (… - …)2;
x2 – 2 . x . 5y + (5y)2 = (x – 5y)2
Vậy: x2 – 10xy + 25y2 = (x – 5y)2
Đề bài tương tự: Chẳng hạn:
4x + 4xy + … = (… + y2)
… - 8xy + y2 = (… - …)2
20. Nhận xét sự đúng, sai của kết quả sau:
x2 + 2xy + 4y2 = (x + 2y)2
Bài giải:
Nhận xét sự đúng, sai:
Ta có: (x + 2y)2 = x2 + 2 . x . 2y + 4y2
= x2 + 4xy + 4y2
Nên kết quả x2 + 2xy + 4y2 = (x + 2y)2 sai.
21. Viết các đa thức sau dưới dạng bình phương của một tổng hoặc một hiệu:
a) 9x2 – 6x + 1; b) (2x + 3y)2 + 2 . (2x + 3y) + 1.
Hãy nêu một đề bài tương tự.
Bài giải:
a) 9x2 – 6x + 1 = (3x)2 – 2 . 3x . 1 + 12 = (3x – 1)2
Hoặc 9x2 – 6x + 1 = 1 – 6x + 9x2 = (1 – 3x)2
b) (2x + 3y) = (2x + 3y)2 + 2 . (2x + 3y) . 1 + 12
= [(2x + 3y) + 1]2
= (2x + 3y + 1)2
Đề bài tương tự. Chẳng hạn:
1 + 2(x + 2y) + (x + 2y)2
4x2 – 12x + 9…
22. Tính nhanh:
a) 1012; b) 1992; c) 47.53.
Bài giải:
a) 1012 = (100 + 1)2 = 1002 + 2 . 100 + 1 = 10201
b) 1992= (200 – 1)2 = 2002 – 2 . 200 + 1 = 39601
c) 47.53 = (50 – 3)(50 + 3) = 502 – 32 = 2500 – 9 = 2491.
23. Chứng minh rằng:
(a + b)2 = (a – b)2 + 4ab;
(a – b)2 = (a + b)2 – 4ab.
Áp dụng:
a) Tính (a – b)2 , biết a + b = 7 và a . b = 12.
b) Tính (a + b)2 , biết a - b = 20 và a . b = 3.
Bài giải:
a) (a + b)2 = (a – b)2 + 4ab
- Biến đổi vế trái:
(a + b)2 = a2 +2ab + b2 = a2 – 2ab + b2 + 4ab
= (a – b)2 + 4ab
Vậy (a + b)2 = (a – b)2 + 4ab
- Hoặc biến đổi vế phải:
(a – b)2 + 4ab = a2 – 2ab + b2 + 4ab = a2 + 2ab + b2
= (a + b)2
Vậy (a + b)2 = (a – b)2 + 4ab
b) (a – b)2 = (a + b)2 – 4ab
Biến đổi vế phải:
(a + b)2 – 4ab = a2 +2ab + b2 – 4ab
= a2 – 2ab + b2 = (a – b)2
Vậy (a – b)2 = (a + b)2 – 4ab
Áp dụng: Tính:
a) (a – b)2 = (a + b)2 – 4ab = 72 – 4 . 12 = 49 – 48 = 1
b) (a + b)2 = (a – b)2 + 4ab = 202 + 4 . 3 = 400 + 12 = 412
24. Tính giá trị của biểu thức 49x2 – 70x + 25 trong mỗi trường hợp sau:
a) x = 5; b) x = .
Bài giải:
49x2 – 70x + 25 = (7x)2 – 2 . 7x . 5 + 52 = (7x – 5)2
a) Với x = 5: (7 . 5 – 5)2 = (35 – 5)2 = 302 = 900
b) Với x = : (7 .
– 5)2 = (1 – 5)2 = (-4)2 = 16
Bài 25. Tính:
a) (a + b + c)2; b) (a + b – c)2;
c) (a – b – c)2
Bài giải:
a) (a + b + c)2 = [(a + b) + c]2 = (a + b)2 + 2(a + b)c + c2
= a2+ 2ab + b2 + 2ac + 2bc + c2
= a2 + b2 + c2 + 2ab + 2bc + 2ac.
b) (a + b – c)2 = [(a + b) – c]2 = (a + b)2 - 2(a + b)c + c2
= a2 + 2ab + b2 - 2ac - 2bc + c2
= a2 + b2 + c2 + 2ab - 2bc - 2ac.
c) (a – b –c)2 = [(a – b) – c]2 = (a – b)2 – 2(a – b)c + c2
= a2 – 2ab + b2 – 2ac + 2bc + c2
= a2 + b2 + c2 – 2ab + 2bc – 2ac.
Bài 26. Tính:
a) (2x2 + 3y)3; b) (x – 3)3
Bài giải:
a) (2x2 + 3y)3 = (2x2)3 + 3(2x2)2 . 3y + 3 . 2x2 . (3y)2 + (3y)3
= 8x6 + 3 . 4x4 . 3y + 3 . 2x2 . 9y2 + 27y3
= 8x6 + 36x4y + 54x2y2 + 27y3
b) (x – 3)3 =
- 3
. 3 + 3
. 32 - 33
= x3 – 3 .
x2 . 3 + 3 .
x . 9 – 27
= x3 –
x2 +
x - 27
Bài 27. Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu:
a) – x3 + 3x2 – 3x + 1;
b) 8 – 12x + 6x2 – x3.
Bài giải:
a) – x3 + 3x2– 3x + 1 = 1 – 3 . 12 . x + 3 . 1 . x2 – x3
= (1 – x)3
b) 8 – 12x + 6x2 – x3 = 23 – 3 . 22. x + 3 . 2 . x2 – x3
= (2 – x)3
Bài 28. Tính giá trị của biểu thức:
a) x3 + 12x2 + 48x + 64 tại x = 6;
b) x3 – 6x2 + 12x- 8 tại x = 22.
Bài giải:
a) x3 + 12x2 + 48x + 64 = x3 + 3 . x2. 4 + 3 . x . 42 + 43
= (x + 4)3
Với x = 6: (6 + 4)3 = 103 = 1000
b) x3 – 6x2 + 12x- 8 = x3 – 3 . x2. 2 + 3 . x . 22 - 23
= (x – 2)3
Với x = 22: (22 – 2)3 = 203 = 8000
Bài 29. Đố: Đức tính đáng quý.
Hãy viết mỗi biểu thức sau dưới dạng bình phương hoặc lập phương của một tổng hoặc một hiệu, rồi điền chữ cùng dòng với biều thức đó vào bảng cho thích hợp. Sau khi thêm dấu, em sẽ tìm ra một trong những đức tính quý báu của con người.
x3 – 3x2 + 3x – 1 N
16 + 8x + x2 U
3x2 + 3x + 1 + x3 H
1 – 2y + y2 Â
Bài giải:
Ta có:
N: x3 – 3x2 + 3x – 1 = x3 – 3 . x2. 1+ 3 . x .12 – 13 = (x – 1)3
U: 16 + 8x + x2= 42 + 2 . 4 . x + x2 = (4 + x)2
= (x + 4)2
H: 3x2 + 3x + 1 + x3 = x3 + 3x2 + 3x + 1
= (x + 1)3 = (1 + x)3
Â: 1 – 2y + y2 = 12 - 2 . 1 . y + y2 = (1 - y)2
= (y - 1)2
Vậy: Đức tính đáng quý là "NHÂN HẬU"
Chú ý:
Có thế khai triển các biểu thức (x – 1)3 , (x + 1)3 , (y - 1)2 , (x + 4)2 ... để tìm xem kết quả ứng với chữ nào và điền vào bảng.
Đúng 0
Bình luận (0)
Ta có:
Áp dụng hằng đăng thức bình phương của một tổng.
\(\left(A+B\right)^2=A^2+2AB+B^2\)
Thay vào sẽ là:
\(\left(4x+1\right)^2=16x^2+8x+1\)
\(\left(a+2\right)^2=a^2+4a+4\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời






