Cho a,b là hai số thực sao cho a^3 + b^3 + ( a+b)^3 + 6ab = 16. Tính a+b
PH
Những câu hỏi liên quan
Cho a, b là các số thực thỏa mãn \(a^3+b^3\) − 6ab = −11. Chứng minh rằng \(\dfrac{-7}{3}\) < a + b < −2
Cho các số thực a,b thoả mãn a 3 +b 3 −6ab = −11. Chứng minh rằng − 7 /3 < a+b < −2
`a^3+b^3-6ab=-11<=>(a+b)^3-3ab(a+b)-6ab=-11<=>(a+b)^3-3ab(a+b+2)=-11`
Đặt `{(S=a+b),(P=ab):}`
Khi đó ta có `S^3-3P(S+2)=-11<=>(4(S^3+11))/(3(S+2))=4P`
Lại có `S^2>=4P` nên `S^2>=(4(S^3+11))/(3(S+2))`
`<=>(S^3-6S^2+44)/(3(S+2))<=0(S\ne-2)`
- TH1:
`{(S^3-6S^2+44<=0),(3(S+2)>0):}<=>`$\begin{cases} S\leq-2,30213805\\S> -2\end{cases}$`<=>-2<S<-2,30213805(` Vô lý `)`
- TH2:
`{(S^3-6S^2+44>=0),(3(S+2)<0):}<=>`$\begin{cases} S\geq-2,30213805\\S< -2\end{cases}$`<=>-2,30213805<S<-2`
mà `-7/3=-2,33333...<-2,30213805` nên `-7/3<S<-2(đfcm)`
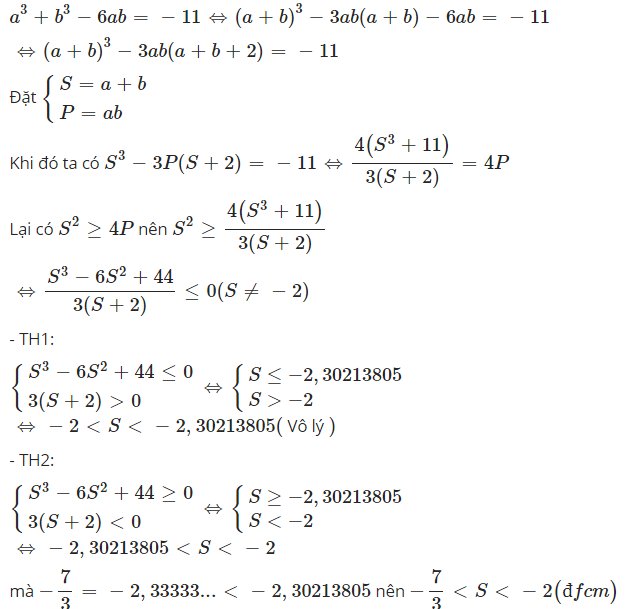
Đúng 1
Bình luận (12)
`a^3+b^3-6ab=-11<=>(a+b)^3-3ab(a+b)-6ab=-11<=>(a+b)^3-3ab(a+b+2)=-11`
Đặt `{(S=a+b),(P=ab):}`
Khi đó ta có `S^3-3P(S+2)=-11<=>(4(S^3+11))/(3(S+2))=4P`
Lại có `S^2>=4P` nên `S^2>=(4(S^3+11))/(3(S+2))`
`<=>(S^3-6S^2+44)/(3(S+2))<=0(S\ne-2)`
- TH1: `{(S^3-6S^2+44<=0),(3(S+2)>0):}<=>{(S<=-2,30213805),(S> -2):}<=>-2<S<-2,30213805(` Vô lý `)`
- TH1: `{(S^3-6S^2+44<=0),(3(S+2)>0):}<=>{(S<=-2,30213805),(S> -2):}<=>-2<S<-2,30213805(` Vô lý `)`
- TH1: `{(S^3-6S^2+44<=0),(3(S+2)>0):}<=>{(S<=-2,30213805),(S> -2):}<=>-2<S<-2,30213805(` Vô lý `)`
- TH1: `{(S^3-6S^2+44<=0),(3(S+2)>0):}<=>{(S<=-2,30213805),(S> -2):}<=>-2<S<-2,30213805(` Vô lý `)`
- TH2: `{(S^3-6S^2+44>=0),(3(S+2)<0):}<=>{(S>=-2,30213805),(S< -2):}<=>-2,30213805<S<-2`
mà `-7/3=-2,33333...<-2,30213805` nên `-7/3<S<-2(đfcm)`
Đúng 0
Bình luận (2)
Xem thêm câu trả lời
Cho hai số \(a,b\) thỏa mãn \(a+b=1\). Hãy tính giá trị của biểu thức
\(P=2a^3+6ab+2b^3-2024\)
\(P=2a^3+2b^3+6ab-2024\)
\(=2\left[\left(a+b\right)^3-3ab\left(a+b\right)\right]+6ab-2024\)
\(=2\left[1-3ab\left(a+b\right)\right]+6ab-2024\)
\(=2-6ab+6ab-2024\)
=-2022
Đúng 0
Bình luận (1)
Cho a+b=1
Tính M= a^3+b^3+3ab (a^2+b^2)+6ab(a+b)
Ta có
a^3+b^3+3ab(a^2+b^2)+6ab(a+b)=a^3+b^3+3ab.a^2+3ab.b^2+6ab=a^3+b^3+3(a^2)b+3(b^2)a+3a(b-1)b^2+3b(a-1)a^2+6ab
=(a+b)^3+3ab((b-1).b+(a-1).a)+6ab=(a+b)^3+3ab((1-b).(-b)+(1-a)(-a))+6ab=(a+b)^3+3ab(-2ab)+6ab
=(a+b)^3+(-6ab)ab+6ab
=>(a+b)^3+6ab(-ab-1)=6ab(-ab-1)+1 Vậy M=6ab(-ab-1)+1
k cho mình nhá
Đúng 0
Bình luận (0)
giúp mik với, thanks mọi người trước nhìu. Bài 1: rút gọn các biểu thức sau: a) ( a + b ) mũ 3 + ( a - b ) mũ 3 - 6ab mũ 2 b ) ( a + b ) mũ 3 - ( a -b ) mũ 3 - 6ab mũ 2 Bài 2: Cho x + y = 7 , tính giá trị biểu thức a) M = ( x + y ) mũ 3 + 2x mxu 2 + 4xy + 2y mỹ 2 b) N = x mũ 3 + y mũ 3 - 2x mũ 2 - 2y mũ 2 + 3xy( x +y) - 4xy + 3(x + y ) =10
Bài 2:
a: Ta có: \(M=\left(x+y\right)^3+2x^2+4xy+2y^2\)
\(=\left(x+y\right)^3+2\cdot\left(x+y\right)^2\)
\(=7^3+2\cdot7^2=441\)
Đúng 0
Bình luận (0)
cho a,b là các số thực dương tm a^3+b^3+6able 8cmr Pa+2b+frac{2}{a}+frac{3}{b}ge8blta có 8ge a^3+b^3+6abge ableft(a+bright)+6abge ableft(a+b+1+1+1+1+1+1right)ge8absqrt[8]{ab}suy ra able1mà Pa+b+b+frac{1}{a}+frac{1}{a}+frac{1}{b}+frac{1}{b}+frac{1}{b}ge8.sqrt[8]{a.b.b.frac{1}{a^2}.frac{1}{b^3}}8sqrt[8]{frac{1}{ab}}ge8dau sảy ra khi ab1
Đọc tiếp
cho a,b là các số thực dương tm \(a^3+b^3+6ab\le\) 8
cmr \(P=a+2b+\frac{2}{a}+\frac{3}{b}\ge8\)
bl
ta có \(8\ge a^3+b^3+6ab\ge ab\left(a+b\right)+6ab\ge ab\left(a+b+1+1+1+1+1+1\right)\ge8ab\sqrt[8]{ab}\)
suy ra ab\(\le1\)
mà P=\(a+b+b+\frac{1}{a}+\frac{1}{a}+\frac{1}{b}+\frac{1}{b}+\frac{1}{b}\ge8.\sqrt[8]{a.b.b.\frac{1}{a^2}.\frac{1}{b^3}}=8\sqrt[8]{\frac{1}{ab}}\ge8\)
dau = sảy ra khi a=b=1
Cho a-b=2.Tính giá trị biểu thức A=a3-b3-6ab
cho a,b,c là các số thực không âm ,a+b+c=3. tìm giá trị nhỏ nhất của biểu thức P=a/(a^3+16)+b/(b^3 +16)+c/(c^3+16)
Ta co:
\(0\le a,b,c\le3\Rightarrow\hept{\begin{cases}a^2\le3a\\b^2\le3b\\c^2\le3c\end{cases}}\Rightarrow\hept{\begin{cases}a^3\le9a\\b^3\le9b\\c^3\le9c\end{cases}}\)
\(\Rightarrow M=\Sigma_{cyc}\frac{a}{a^3+16}\ge\Sigma_{cyc}\frac{a}{9a+16}=\Sigma_{cyc}\frac{a^2}{9a^2+16a}\ge\frac{\left(a+b+c\right)^2}{9\left(a^2+b^2+c^2\right)+16\left(a+b+c\right)}\)
\(\Rightarrow M\ge\frac{\left(a+b+c\right)^2}{27\left(a+b+c\right)+16\left(a+b+c\right)}=\frac{3}{43}\)
Dau '=' xay ra khi \(\left(a;b;c\right)=\left(0;0;3\right)=\left(3;0;0\right)=\left(0;3;0\right)\)
cách làm này vẫn có 1 số chỗ không rõ
cho a,b là hai số thực sao cho \(a^3+b^3=2\) chứng minh
0 < a +b =< 2
Giả sử a+b >2 thì a3+b3+3ab(a+b)>8a3+b3+3ab(a+b)>8
⇔ab(a+b)>2⇔ab(a+b)>2
⇔ab(a+b)>a3+b3⇔ab(a+b)>a3+b3
⇔(a−b)2(a+b)<0⇔(a−b)2(a+b)<0
vô lý nên a+b≤2a+b≤2
Đúng 0
Bình luận (0)
a3+b3=(a+b)(.....)
dễ có (...) >0 => a+b>0
kia thì áp dụng bđt 4(a3+b3)>=(a+b)3 (dễ cm mà ,,,tách a^3+b^3 ra rồi cói và bđt phụ)
Đúng 0
Bình luận (0)



