Viết lại các đa thức thành vế kia hằng đẳng thức
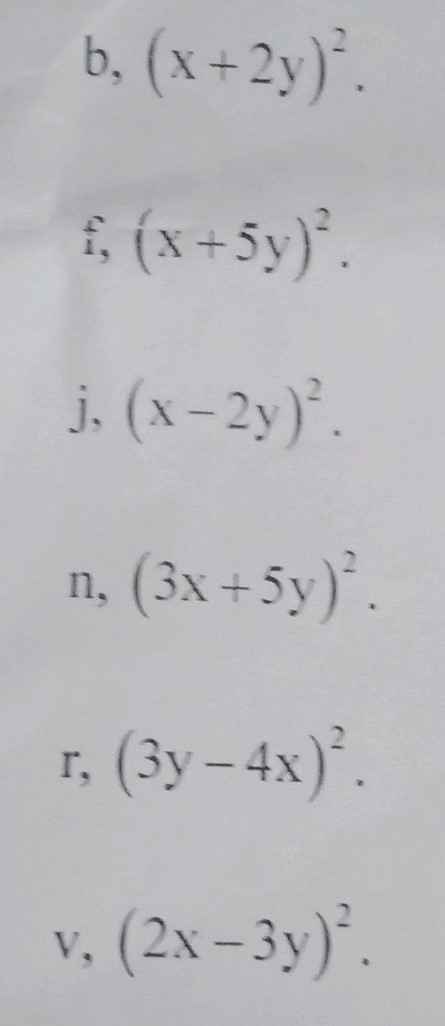
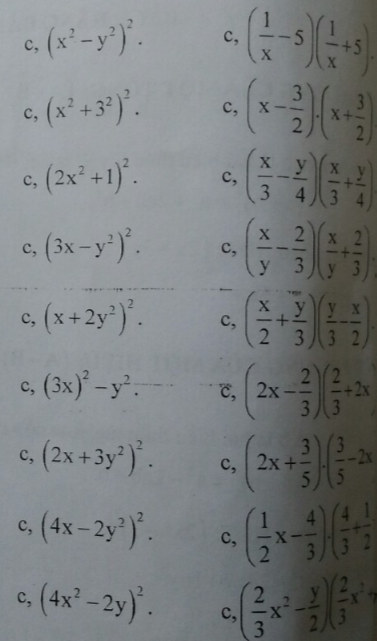 viết lại các đa thức thành các vế kia hằng đẳng thức giúp em với ạ em đang cần gấp
viết lại các đa thức thành các vế kia hằng đẳng thức giúp em với ạ em đang cần gấp
c) \(\left(x^2-y^2\right)^2=x^4-2x^2y^2+y^4\)
c) \(\left(x^2+3^2\right)^2=x^4+18x+81\)
c) \(\left(2x^2+1\right)^2=4x^4+4x^2+1\)
c) \(\left(3x-y^2\right)^2=9x^2-6xy^2+y^4\)
c) \(\left(x+2y^2\right)^2=x^2+4xy^2+4y^4\)
c) \(\left(3x\right)^2-y^2=\left(3x-y\right)\left(3x+y\right)\)
c) \(\left(2x+3y^2\right)^2=4x^2+12xy^2+9y^4\)
c) \(\left(4x-2y^2\right)^2=16x^2-16xy^2+4y^4\)
c) \(\left(4x^2-2y\right)^2=16x^4-16x^2y+4y^2\)
c) \(\left(\dfrac{1}{x}-5\right)\left(\dfrac{1}{x}+5\right)=\dfrac{1}{x^2}-25\)
c) \(\left(x-\dfrac{3}{2}\right)\left(x+\dfrac{3}{2}\right)=x^2-\dfrac{9}{4}\)
c) \(\left(\dfrac{x}{3}-\dfrac{y}{4}\right)\left(\dfrac{x}{3}+\dfrac{y}{4}\right)=\dfrac{x^2}{9}-\dfrac{y^2}{16}\)
c) \(\left(\dfrac{x}{y}-\dfrac{2}{3}\right)\left(\dfrac{x}{y}+\dfrac{2}{3}\right)=\dfrac{x^2}{y^2}-\dfrac{4}{9}\)
c) \(\left(\dfrac{x}{2}+\dfrac{y}{3}\right)\left(\dfrac{y}{3}-\dfrac{x}{2}\right)=\dfrac{y^2}{9}-\dfrac{x^2}{4}\)
c) \(\left(2x-\dfrac{2}{3}\right)\left(\dfrac{2}{3}+2x\right)=4x^2-\dfrac{4}{9}\)
c) \(\left(2x+\dfrac{3}{5}\right)\left(\dfrac{3}{5}-2x\right)=\dfrac{9}{25}-4x^2\)
c) \(\left(\dfrac{1}{2}x-\dfrac{4}{3}\right)\left(\dfrac{4}{4}+\dfrac{1}{2}x\right)=\dfrac{1}{4}x^2-\dfrac{16}{9}\)
c) \(\left(\dfrac{2}{3}x^2-\dfrac{y}{2}\right)\left(\dfrac{2}{3}x^2+\dfrac{y}{2}\right)=\dfrac{4}{9}x^4-\dfrac{y^2}{4}\)
viết lại đa thức thành vế kia hằng đẳng thức
(x2 + 32)2
(x2 + 32)2
=x^4 + 18x^2+81
(x2 + 32)2
= (x2)2 + 2x2 . 32 + (32)2
= x4 + 18x2 + 81
Viết lại đa thức thành vế kia hằng đẳng thức
a. (2x - 3y)^2
b (3\(\sqrt{x}\)- y)^2
( 2x - 3y )2 = 4x2 - 12xy + 9y2
( 3√x - y )2 = 9x - 6y√x + y2 ( x ≥ 0 )
2: Viết lại các đa thức thành vế kia hằng đẳng thức:
a, 4x^(4)-4x^(2)+16
b, (x+2y)^(2).
c, 36+x^(2)-12xy
d, (x+5y)^(2).
e, 4x^(2)-12x+9
f,(x-2y)^(2).
\(4x^4-4x^2+1=\left(2x^2-1\right)^2\)
\(\left(x+2y\right)^2=x^2+4xy+4y^2\)
\(36-12x+x^2=\left(6-x\right)^2\)
\(\left(x+5y\right)^2=x^2+10xy+25y^2\)
\(4x^2-12x+9=\left(2x-3\right)^2\)
\(\left(x-2y\right)^2=x^2-4xy+4y^2\)
viết lại đa thức thành vế kia hằng đẳng thức
a/ 36+x^2 - 12x
b/ (x+2y)^2
c/(\(\sqrt{x}\)-2\(\sqrt{y}\))^2
a/ \(36+x^2-12x=x^2-2x.6+6^2=\left(x+6\right)^2\)
b/ \(\left(x+2y\right)^2=x^2+2x.2y+\left(2y\right)^2=x^2+4xy+4y^2\)
c/ \(\left(\sqrt{x}-2\sqrt{y}\right)^2=\left(\sqrt{x}\right)^2-2\sqrt{x}.2\sqrt{y}+\left(2\sqrt{y}\right)^2=x-4\sqrt{xy}+4y\)
viết lại đa thức thành vế kia hằng đẳng thức
a. (\(\frac{x}{y}\)-\(\frac{2}{3}\)) (\(\frac{x}{y}\)+\(\frac{2}{3}\))
b. (2\(\sqrt{x}\) - \(\frac{2}{3}\)) (\(\frac{2}{3}\) + 2\(\sqrt{x}\))
a, \(\left(\frac{x}{y}-\frac{2}{3}\right)\left(\frac{x}{y}+\frac{2}{3}\right)=\left(\frac{x}{y}\right)^2-\left(\frac{2}{3}\right)^2\)
b,\(\left(2\sqrt{x}-\frac{2}{3}\right)\left(\frac{2}{3}+2\sqrt{x}\right)=\left(2\sqrt{x}-\frac{2}{3}\right)\left(2\sqrt{x}+\frac{2}{3}\right)\)
\(=\left(2\sqrt{x}\right)^2-\left(\frac{2}{3}\right)^2\)
Trả lời:
a, \(\left(\frac{x}{y}-\frac{2}{3}\right)\left(\frac{x}{y}+\frac{2}{3}\right)\)\(=\left(\frac{x}{y}\right)^2-\left(\frac{2}{3}\right)^2=\frac{x^2}{y^2}-\frac{4}{9}\)
b, \(\left(2\sqrt{x}-\frac{2}{3}\right)\left(\frac{2}{3}+2\sqrt{x}\right)=\left(2\sqrt{x}-\frac{2}{3}\right)\left(2\sqrt{x}+\frac{2}{3}\right)=\left(2\sqrt{x}\right)^2-\left(\frac{2}{3}\right)^2=4x-\frac{4}{9}\)
Dùng bút chì nối các biểu thức sao cho chúng tạo thành hai vế của một hằng đẳng thức (theo mẫu):
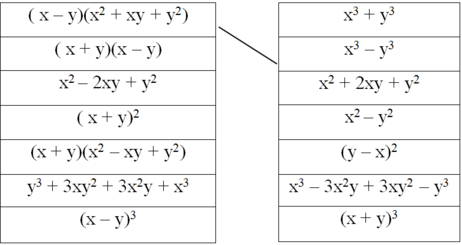
viết vế còn lại của hằng đẳng thức
4x^2-20xy^2+25Y^4
\(4x^2-20xy^2+25y^4=\left(2x\right)^2-2.2x.5y^2+\left(5y^2\right)^2=\left(2x-5y^2\right)^2\)
Áp dụng hằng đẳng thức: \(\left(A-B\right)^2=A^2-2AB+B^2\)
\(4x^2-20xy^2+25y^4\)
\(=\left(2x\right)^2-2\cdot2x\cdot5y^2+\left(5y\right)^2\)
\(=\left(2x-5y\right)^2\)
\(4x^2-20xy^2+25y^4\)
\(=\left(2x\right)^2-2.2.5.xy^2+\left(5y\right)^2\)
\(=\left(2x-5y\right)^2\)
Viết thành vế kia xủa đẳng thức a, 8x^3-12x^2+6x-1
Giúp mk với , mk ko lm đc.
\(8x^3-12x^2+6x-1=\left(2x-1\right)^3\)
Bổ sung vế còn lại để tạo thành hằng đẳng thức đúng:
(y-5).(y2+5y+25)
\(\left(y-5\right).\left(y^2+5y+25\right)=y^3-5^3=y^3-125\)