Trên đường thẳng a cho điểm n phân biệt ( n \(\in\) N; n > 1 Dếm được 820 đoạn thẳng Hãy tìm n
TT
Những câu hỏi liên quan
Trên đường thẳng a cho điểm n phân biệt( n \(\in\) N; n> 1) Đếm được 820 đoạn thẳng Hãy tìm n
Ta có :
Cứ n điểm thì tạo được với n - 1 điểm còn khác tạo thành n - 1 đường thẳng . Trên thực tế , số đường thẳng này đã được ta tính 2 lần . Vì vậy có số đường thẳng là :
\(\frac{n\left(n-1\right)}{2}\) đường thẳng
=> \(\frac{n\left(n-1\right)}{2}=820\)
=> n( n - 1 ) = 1640
=> n = 41
Vậy có 41 điểm
Đúng 0
Bình luận (0)
Ta có:
Cứ n điểm thì tạo được với n - 1 điểm còn khác tạo thành n - 1 đường thẳng. Trên thực tế, sô đường thẳng này đã được ta tính 2 lần. Vì vậy có số đường thẳng là: \(\frac{n\left(n-1\right)}{2}\) đường thẳng
=>\(\frac{n\left(n-1\right)}{2}\) = 820
=> n ( n - 1 ) = 1640
=> n = 41
Vậy có 41 điểm
Đúng 0
Bình luận (0)
a) Cho n điểm phân biệt trong đó ko có ba điểm nào thẳng hàng kẻ các đường thẳng đi qua các cặp điểm . Hỏi có bao nhiêu đường thẳng ?
b) Nếu qua n đểm trên kẻ được 28 đường thẳng thì n = ? ( n \(\in\)N*)
Công thức là n.(n + 1) / 2
Theo bài ra ta có: n.(n + 1) / 2 = 28
=> n.(n + 1) = 56
=> n . (n + 1) = 7.8
=> n = 7
Vậy n = 7
Đúng 0
Bình luận (0)
a. Câu hỏi của Hà Nhật Anh - Toán lớp 6 - Học toán với OnlineMath
a,Cho 5 điểm phân biệt, trong đó không có ba điểm nào thẳng hàng.Cứ qua hai điểm, ta kẻ một đường thẳng. Có tất cả bao nhiêu đường thẳng ?b,Cũng như câu hỏi trên đối với n điểm phân biệt, trong đó không có ba điểm nào thẳng hàng.c,Cho n điểm phân biệt, trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm trong n điểm đó ta kẻ một đường thẳng, biết rằng có 66 đường thẳng. Tìm n
Đọc tiếp
a,Cho 5 điểm phân biệt, trong đó không có ba điểm nào thẳng hàng.Cứ qua hai điểm, ta kẻ một đường thẳng. Có tất cả bao nhiêu đường thẳng ?
b,Cũng như câu hỏi trên đối với n điểm phân biệt, trong đó không có ba điểm nào thẳng hàng.
c,Cho n điểm phân biệt, trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm trong n điểm đó ta kẻ một đường thẳng, biết rằng có 66 đường thẳng. Tìm n
ai đó giúp tớ với
AI LÀM NHANH VÀ ĐÚNG TỚ K CHO
a , Ta kẻ được 10 đoạn thẳng .
Giúp mình với.Mình tick cho
a) Cho 4 điểm phân biệt ko có 3 điểm nào thẳng hàng.Có bao nhiêu đường thẳng đi qua 2 trong 4 điểm trên
b) Cho 8 điểm phân biệt ko có 3 điểm nào thẳng hàng.Có bao nhiêu đường thẳng đi qua 2 trong 8 điểm trên
c) Cho n điểm phân biệt ko có 3 điểm nào thẳng hàng.Có bao nhiêu đường thẳng đi qua 2 trong n điểm trên
a, 6 đường thẳng
b, 28 đường thẳng
c, \(\frac{n.\left(n-1\right)}{2}\)đường thẳng
Đúng 0
Bình luận (0)
Giúp tui vs, tui cần rất gấp, gấp lắm luôn áa) cho 5 điểm phân biệt, trong đó không có ba điểm nào thẳng hàng. Cứ hai điểm , ta kẻ một đường thẳng. có tất cả bao nhiêu đường thẳng?b) Cũng như câu hỏi trên đối với n điểm phân biệt, trong đó không có ba điểm nào thẳng hàng.c) Cho n điểm phân biệt, trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm trong n điểm đó ta kẻ một đường thẳng. Biết rằng có 66 đường thẳng. Tìm n
Đọc tiếp
Giúp tui vs, tui cần rất gấp, gấp lắm luôn á
a) cho 5 điểm phân biệt, trong đó không có ba điểm nào thẳng hàng. Cứ hai điểm , ta kẻ một đường thẳng. có tất cả bao nhiêu đường thẳng?
b) Cũng như câu hỏi trên đối với n điểm phân biệt, trong đó không có ba điểm nào thẳng hàng.
c) Cho n điểm phân biệt, trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm trong n điểm đó ta kẻ một đường thẳng. Biết rằng có 66 đường thẳng. Tìm n
a,có tất cả 10 đg thẳng
b,n(n-1)/2 đg thẳng
c.n(n-1)/2=66
n(n-1)=132
n=12
Đúng 0
Bình luận (0)
a) 5 duong thang
b) thi co n duong thang
c) 66 duong thang
vi co bao nhieu diem thi co bay nhieu duong thang di qua ( khi 3 diem ko thang hang)
tuong tu vs duong thang nha
Đúng 0
Bình luận (0)
nghi don gian thoi
ko can nghi nhieu sai day tui cx lop 6 ma
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a, cho n điểm phân biệt trong đó ko có 3 điểm nào thẳng hàng kẻ các đường thẳng đi qua các cặp điểm . hỏi có ? đường thẳng
b, nếu qua n điểm trên kẻ được 28 đường thẳng thì n=? ( n thuộc N)
Câu hỏi của Hà Nhật Anh - Toán lớp 6 - Học toán với OnlineMath
Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt n
≥
2 . Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n? A. 20 B. 21 C. 30 D. 32
Đọc tiếp
Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt n ≥ 2 . Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n?
A. 20
B. 21
C. 30
D. 32
Tam giác cần lập thuộc hai loại
Loại 1: Tam giác có một đỉnh thuộc d1 và hai đỉnh thuộc d2. Loại này có ![]() tam giác.
tam giác.
Loại 2: Tam giác có một đỉnh thuộc d2 và hai đỉnh thuộc d1. Loại này có ![]() tam giác.
tam giác.
Theo bài ra ta có: ![]()
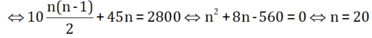
Chọn A.
Đúng 0
Bình luận (0)
Cho hai đường thẳng
d
1
và
d
2
song song với nhau. Trên
d
1
có 10 điểm phân biệt, trên
d
2
có n điểm phân biệt (
n
≥
2
). Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n? A. 16 B. 21 C. 30 D. 20
Đọc tiếp
Cho hai đường thẳng d 1 và d 2 song song với nhau. Trên d 1 có 10 điểm phân biệt, trên d 2 có n điểm phân biệt ( n ≥ 2 ). Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n?
A. 16
B. 21
C. 30
D. 20
Tam giác cần lập thuộc hai loại
Loại 1: Tam giác có một đỉnh thuộc d 1 và hai đỉnh thuộc d 2 .
Loại này có C 10 1 . C n 2 tam giác.
Loại 2: Tam giác có một đỉnh thuộc d 2 và hai đỉnh thuộc d 1 .
Loại này có C 10 2 . C n 1 tam giác.
Theo bài ra ta có: C 10 1 . C n 2 + C 10 2 . C n 1 = 2800
⇔ 10 n ( n − 1 ) 2 + 45 n = 2800 ⇔ n 2 + 8 n − 560 = 0 ⇔ n = 20
Chọn đáp án D
Đúng 0
Bình luận (0)
Cho n điểm phân biệt thuộc đường thẳng a và một điểm nằm ngòai đường thẳng ấy . Có bao nhiêu tam giác có các đỉnh là ba trong n+1 điểm trên



