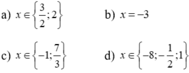Giải phương trình sau: (12x+7)2(3x+2)(2x+1) = 3
SK
Những câu hỏi liên quan
Giải các phương trình sau:
a,2x(8x-1)2(4x-1)=9
b,(12x+7)2(3x+2)(2x+1)=3
c,(2x+1)(x+1)2(2x+3)=18
a,2x(8x-1)2(4x-1)=9(1)
<=>(8x-2)(8x-1)2.x=9
<=>8x(8x-1)2(8x-2)=8.9=72(2)
Đặt 8x-1=y ,pt (2) trở thành (y+1)y2(y-1)=72 ....... tới đây tự giải
b, tương tự ý a ,nhan 4 vào (3x+2) ,nhân 6 vào (2x+3)
c, nhân 2 vào (x+1)
Đúng 1
Bình luận (0)
Giải phương trình sau
a) \(\sqrt{\left(2x-5\right)^2}=7\)
b) \(\sqrt{3x}-\sqrt{12x}=\sqrt{27}-\sqrt{48}\)
(a) Phương trình tương đương: \(\left|2x-5\right|=7\)
\(\Rightarrow\left[{}\begin{matrix}2x-5=7\\2x-5=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-1\end{matrix}\right.\).
Vậy: \(S=\left\{-1;6\right\}\)
(b) Điều kiện: \(x\ge0\).
Phương trình tương đương: \(\sqrt{3x}-2\sqrt{3x}=3\sqrt{3}-4\sqrt{3}\)
\(\Leftrightarrow\sqrt{3}\left(\sqrt{x}-2\sqrt{x}\right)=-\sqrt{3}\)
\(\Leftrightarrow\sqrt{x}-2\sqrt{x}=-1\)
\(\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(TM\right)\).
Vậy: \(S=\left\{1\right\}\)
Đúng 1
Bình luận (0)
Giải Phương Trình:
\(\left(12x+7\right)^2\left(3x+2\right)\left(2x+1\right)=3\)
Giải các phương trình sau:
a \(x^4=5x^2+2x-3\)
b \(x^4=6x^2+12x+10\)
c \(3x^3+3x^2+3x=-1\)
d \(8x^3-12x^2+6x-5=0\)
1) Giải các phương trình sau : a) x-3/x=2-x-3/x+3 b) 3x^2-2x-16=0 2) Giải bất phương trình sau: 4x-3/4>3x-5/3-2x-7/12
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
Đúng 1
Bình luận (0)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
Đúng 1
Bình luận (0)
Giải các phương trình sau:
1) \(\sqrt{2x+4}-2\sqrt{2-x}=\dfrac{12x-8}{\sqrt{9x^2+16}}.\)
2) \(\sqrt{3x^2-7x+3}-\sqrt{x^2-2}=\sqrt{3x^2-5x-1}-\sqrt{x^2-3x+4}.\)
Giải phương trình:
3
x
-
2
x
+
7
6
x
+
1
2
x
-...
Đọc tiếp
Giải phương trình: 3 x - 2 x + 7 = 6 x + 1 2 x - 3
Điều kiện xác định: x ≠ -7; x ≠ 3/2.
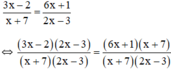
Suy ra: (3x – 2)(2x – 3) = (6x + 1)(x + 7)
⇔ 6x2 – 9x – 4x + 6 = 6x2 + 42x + x + 7
⇔ - 4x - 9x - 42x - x = 7 - 6
⇔ - 56x = 1
⇔ x = -1/56 (thỏa mãn đkxđ)
Vậy phương trình có tập nghiệm S = {-1/56}.
Đúng 0
Bình luận (0)
Giải các phương trình sau:
a) (x+2)^3-(x-2)^3=12x(x-1)-8
b) (3x-1)^2-5(2x+1)^2+(6x-3)(2x+1)= (x-1)^2
Giai giúp mik với
Giải phương trình:
a) (x+2)3 - (x-2)3 = 12x(x-1) - 8
<=> (x2 + 3.x2.2 + 3.x.22 + 23) - (x2 - 3.x2.2 + 3.x.22 - 23) - [12x(x-1) - 8] = 0
<=> (x3 + 6x2 + 12x + 8) - (x3 - 6x2 + 12x - 8) - (12x2 - 12x - 8) = 0
<=> x3 + 6x2 + 12x + 8 - x3 + 6x2 - 12x + 8 - 12x2 + 12x + 8 = 0
<=> 12x +32 = 0
<=> x = \(\frac{-32}{12}\) = \(-2\frac{2}{3}\)
Vậy phương trình có nghiệm duy nhất là \(-2\frac{2}{3}\)
b) (3x-1)2 - 5(2x+1)2 + (6x-3)(2x+1) = (x-1)2
<=> (9x2 - 6x + 1) - 5(4x2 + 4x + 1) + 3(2x - 1)(2x + 1) - (x2 - 2x +1) = 0
<=> 9x2 - 6x + 1 - 20x2 - 20x - 5 + 3(4x2 - 1) - x2 + 2x -1 = 0
<=> 9x2 - 6x + 1 - 20x2 - 20x - 5 + 12x2 - 3 - x2 + 2x -1 = 0
<=> -24x - 8 = 0
<=> x = \(\frac{-8}{24}\) = \(\frac{-1}{3}\)
Vậy phương trình có nghiệm duy nhất là \(\frac{-1}{3}\)
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
x
−
1
3
x
−
5
;b)
x
+
1
2
+
1
x
+
3...
Đọc tiếp
Giải các phương trình sau:
a) x − 1 = 3 x − 5 ;
b) x + 1 2 + 1 x + 3 = 0 ;
c) 3 x 2 − 4 x − 7 = 0 ;
d) 7 x − 1 2 x + 1 + 2 x + 1 x 2 − 1 = 0 .