số trục đối xứng của K
H24
Những câu hỏi liên quan
Cho điểm \(M\left( {{x_0};{y_0}} \right)\). Tìm tọa độ
a) Điểm H là hình chiếu vuông góc của M trên trục Ox
b) Điểm M’ đối xứng với M qua trục Ox
c) Điểm K là hình chiếu vuông góc của M trên trục Oy
d) Điểm M’’ đối xứng với M qua trục Oy
e) Điểm C đối xứng với M qua gốc tọa độ
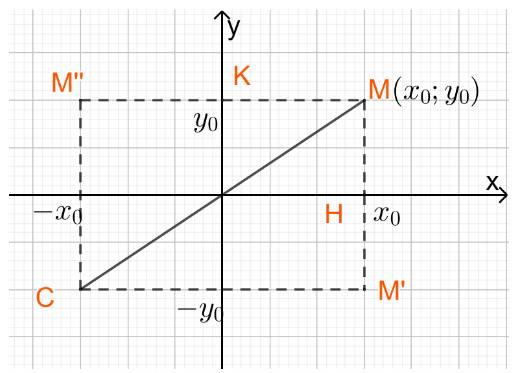
a) H là hình chiếu vuông góc của M trên trục Ox nên tọa độ điểm H là \(H\left( {{x_0};0} \right)\)
b) M’ đối xứng với M qua trục Ox nên H là trung điểm của MM’
Suy ra \({x_{M'}} = 2{x_H} - {x_M} = 2{x_0} - {x_0} = {x_0};{y_{M'}} = 2{y_H} - {y_M} = 2.0 - {y_0} = - {y_0}\)
Vậy tọa độ điểm M’ là \(\left( {{x_0}; - {y_0}} \right)\)
c) K là hình chiếu vuông góc của M trên trục Oy nên tọa độ điểm K là \(K\left( {0;{y_0}} \right)\)
d) M’’ đối xứng với M qua trục Oy nên K là trung điểm của MM’’
Suy ra \({x_{M''}} = 2{x_K} - {x_M} = 2.0 - {x_0} = - {x_0};{y_{M''}} = 2{y_K} - {y_M} = 2{y_0} - {y_0} = {y_0}\)
Vậy tọa độ điểm M'' là \(\left( { - {x_0};{y_0}} \right)\)
e) C đối xứng với M qua gốc tọa độ nên O là trung điểm của MC
Suy ra \({x_C} = 2{x_O} - {x_M} = 2.0 - {x_0} = - {x_0};{y_C} = 2{y_O} - {y_M} = 2.0 - {y_0} = - {y_0}\)
Vậy tọa độ điểm C là \(\left( { - {x_0}; - {y_0}} \right)\)
Đúng 0
Bình luận (0)
Số phát biểu sai:a) Phép đối xứng trục là một phép dời hìnhb) Đường thẳng d được gọi là trục đối xứng của hình (H) nếu phép đối xứng trục Đd biến hình (H) thành chính nó.c) Một hình có thể có một hay nhiều trục đối xứng, có thể không có trục đối xứng.d) Qua phép đối xứng trục, đoạn thẳng AB biến thành đoạn thẳng song song và bằng nó.e) Qua phép đối xứng trục Đa, đường tròn có tâm nằm trên a sẽ biến thành chính nó.f) Qua phép đối xứng trục Đa, tam giác có một đỉnh nằm trên a sẽ biến thành chính n...
Đọc tiếp
Số phát biểu sai:
a) Phép đối xứng trục là một phép dời hình
b) Đường thẳng d được gọi là trục đối xứng của hình (H) nếu phép đối xứng trục Đd biến hình (H) thành chính nó.
c) Một hình có thể có một hay nhiều trục đối xứng, có thể không có trục đối xứng.
d) Qua phép đối xứng trục, đoạn thẳng AB biến thành đoạn thẳng song song và bằng nó.
e) Qua phép đối xứng trục Đa, đường tròn có tâm nằm trên a sẽ biến thành chính nó.
f) Qua phép đối xứng trục Đa, tam giác có một đỉnh nằm trên a sẽ biến thành chính nó
g) Qua phép đối xứng trục Đa, ảnh của đường thẳng vuông góc với a là chính nó
h) Nều phép đối xứng trục biến đường thẳng a thành đường thẳng b cắt a thì giao điểm của a và b nằm trên trục đối xứng
i) Hình chữ nhật có 4 trục đối xứng
A. 3
B.5
C. 7
D.9
Đáp án A
Nhữngphát biểu sai: d; f; i
d) Qua phép đối xứng trục, đoạn thẳng AB biến thành đoạn thẳng song song và bằng nó hoặc là chính nó.
f) Qua phép đối xứng trục Đa, tam giác có một đỉnh nằm trên a sẽ biến thành chính nó ( chỉ trong trường hợp tam giác đều hoặc tam giác cân cóđỉnh nằm trên trục đối xứng)
i) Hình chữ nhật có 2 trục đối xứng
Đúng 0
Bình luận (0)
Đường tròn là hình. Chọn khẳng định đúng:
a, Không có trục đối xứng
b, Có một trục đối xứng
c, Có hai trục đối xứng
d, Có vô số trục đối xứng
Số trục đối xứng của hình vuông là
A 1
B 2
C 4
D 8
Số trục đối xứng của hình tròn là
A 1
B 2
C 4
D vô số
Này Vuông, tớ nghĩ cậu có hai trục đối xứngTớ lại nghĩ tớ có vô số trục đối xứng cơ!Hình Tròn là tớ đây mới có vô số trục đối xứng!Các bạn ơi, giúp tớ với!• Hình vuông có bao nhiêu trục đối xứng?• Hình tròn có bao nhiêu trục đối xứng?
Đọc tiếp
Này Vuông, tớ nghĩ cậu có hai trục đối xứng

Tớ lại nghĩ tớ có vô số trục đối xứng cơ!

Hình Tròn là tớ đây mới có vô số trục đối xứng!

Các bạn ơi, giúp tớ với!

• Hình vuông có bao nhiêu trục đối xứng?
• Hình tròn có bao nhiêu trục đối xứng?
* Hình vuông có 4 trục đối xứng gồm 2 đường chéo của hình vuông và 2 đường thẳng đi qua trung điểm từng của cặp cạnh đối diện của hình vuông
* Hinh tròn có vô số trục đối xứng là các đường thẳng đi qua tâm của hình vuông.
Đúng 0
Bình luận (0)
Cho các mệnh đề sau:
1. Tam giác đều có 3 trục đối xứng và 1 tâm đối xứng
2. Hình vuông có 4 trục đối xứng và 1 tâm đối xứng
3. Ngũ giác đều có 5 trục đối xứng và 1 tâm đối xứng
4. Lục giác đều có 6 trục đối xứng và 1 tâm đối xứng
Số mệnh đềđúng là:
A.1
B.2
C.3
D.4
Các phát biểu nào sai?
A. Hình tròn có vô số trục đối xứng và 1 tâm đối xứng
B. Hình vuông có 4 trục đối xứng
C. Hình tam giác đều có 3 trục đối xứng 1 tâm đối xứng
D. Hình lục giác đều có 1 tâm đối xứng và 6 trục đối xứng
Các phát biểu về đối xứng hình học như sau:
A. Hình tròn: Hình tròn có vô số trục đối xứng và 1 tâm đối xứng. Điều này đúng.
B. Hình vuông: Hình vuông có 4 trục đối xứng, tương ứng với 4 đường đối xứng qua các đỉnh của hình vuông. Điều này cũng đúng.
C. Hình tam giác đều: Hình tam giác đều có 3 trục đối xứng và 1 tâm đối xứng. Điều này cũng đúng.
D. Hình lục giác đều: Hình lục giác đều có 1 tâm đối xứng và 6 trục đối xứng, tương ứng với 6 đường đối xứng qua các đỉnh của hình lục giác đều. Điều này cũng đúng.
Vậy tất cả các phát biểu đều đúng. 😊
Đúng 0
Bình luận (0)
Các tứ giác sau có bao nhiêu trục đối xứng, bao nhiêu tâm đối xứng?Tứ giác: ___ trục đối xứng, ___ tâm đối xứngHình thang: ___ trục đối xứng, ___ tâm đối xứngHình thang cân: ___ trục đối xứng, ___ tâm đối xứngHình binh hành: ___ trục đối xứng, ___ tâm đối xứngHình chữ nhật: ___ trục đối xứng, ___ tâm đối xứngHình thoi: ___ trục đối xứng, ___ tâm đối xứngHình vuông: ___ trục đối xứng, ___ tâm đối xứng
Đọc tiếp
Các tứ giác sau có bao nhiêu trục đối xứng, bao nhiêu tâm đối xứng?
Tứ giác: ___ trục đối xứng, ___ tâm đối xứng
Hình thang: ___ trục đối xứng, ___ tâm đối xứng
Hình thang cân: ___ trục đối xứng, ___ tâm đối xứng
Hình binh hành: ___ trục đối xứng, ___ tâm đối xứng
Hình chữ nhật: ___ trục đối xứng, ___ tâm đối xứng
Hình thoi: ___ trục đối xứng, ___ tâm đối xứng
Hình vuông: ___ trục đối xứng, ___ tâm đối xứng
Tứ giác: 0 trục, 0 tâm
Hình thang 0 trục, 0 tâm
Hình thang cân 1 trục 0 tâm
Hình bình hành 0 trục 1 tâm
Hình chữ nhật 2 trục 1 tâm
Hình thoi 2 trục 1 tâm
Hình vuông 4 trục 1 tâm
Đúng 2
Bình luận (0)
Tứ giác: 0 trục đối xứng, 0 tâm đối xứng
Hình thang: 0 trục đối xứng, 0 tâm đối xứng
Hình thang cân: 1 trục đối xứng, 0 tâm đối xứng
Hình bình hành: 0 trục đối xứng, 1 tâm đối xứng
Hình chữ nhật: 2 trục đối xứng, 1 tâm đối xứng
Hình thoi: 2 trục đối xứng, 1 tâm đối xứng
Hình vuông: 4 trục đối xứng, 1 tâm đối xứng
Tích đúng 5 sao cho mình nhé.
OK bạn
Đúng 2
Bình luận (0)
1. Những chữ cái nào dưới đây có trục đối xứng? Hãy dự đoán trục đối xứng của chúng.2. Những hình nào dưới đây có trục đối xứng?3. Hãy tìm một ví dụ khác về hình có trục đối xứng.
Đọc tiếp
1. Những chữ cái nào dưới đây có trục đối xứng? Hãy dự đoán trục đối xứng của chúng.

2. Những hình nào dưới đây có trục đối xứng?
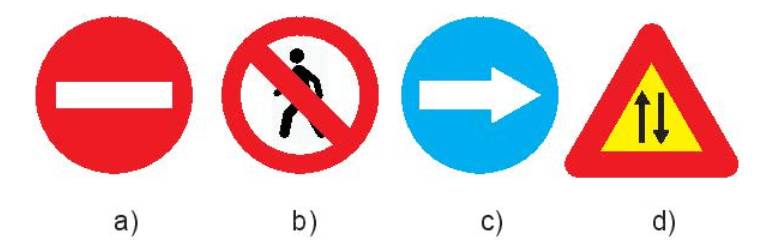
3. Hãy tìm một ví dụ khác về hình có trục đối xứng.
1. Những hình có trục đối xứng là: A, H, E
+ Chữ A có một trục đối xứng như sau:

+ Chữ H có 2 trục đối xứng:
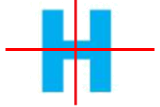
+ Chữ E có 1 trục đối xứng:

2. Những hình có trục đối xứng là: a) và c)
+) Với biển báo a) “cấm đi ngược chiều”: trục đối xứng là đường thẳng đứng và đường nằm ngang đi qua tâm của biển báo.

+) Với biển báo c) “chỉ hướng phải đi theo”: trục đối xứng là đường nằm ngang đi qua tâm của biển báo.

3. Một số ví dụ về hình có trục đối xứng: mặt bàn, cái mâm, viên bi, chiếc bảng, khung cửa sổ, …
Các chữ cái: I, O, M, số 0, số 8,….có trục đối xứng.
Minh họa bằng 1 hình ảnh có trục đối xứng:

Đúng 1
Bình luận (0)
Vẽ các chữ cái in hoa có trục đối xứng và số trục đối xứng
Tất cả các chữ in hoa có đối xứng trục: W, E, T, Y, U, I, O, A, Â, Ă, D, H, X, C, V, B, M.
Đúng 0
Bình luận (0)





