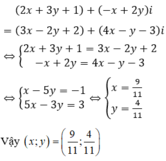Cho x,y là các số thực thỏa mãn x+y=1. Tính \(A=x^4+y^4-2x^3-2x^2y^2+x^2-2y^3+y^2\)
TT
Những câu hỏi liên quan
Tìm các số thực x, y thỏa mãn:
a) 2x + 1 + (1 – 2y)i = 2 – x + (3y – 2)i
b) 4x + 3 + (3y – 2)i = y +1 + (x – 3)i
c) x + 2y + (2x – y)i = 2x + y + (x + 2y)i
Chờ x, y là các số thực thỏa mãn :x^2 + y^2, x+y,x^4 + y^4 là các số nguyên.C/m 2x^2y^2,x^3 +y^3 cũng là các số nguyên
Cho x,y là số thực thỏa mãn x+y=1. Tính min P = \(2x^4+x^3\left(2y-1\right)+y^3\left(2x-1\right)+2y^4\)
Sau khi thay thế y = 1 - x. Ta được:
\(P=3x^2-3x+1=\frac{3}{4}\left(2x-1\right)^2+\frac{1}{4}\ge\frac{1}{4}\)
Đẳng thức xảy ra khi \(x=y=\frac{1}{2}\)
Cho x,y là các số thực thỏa mãn x+y=1. Tìm GTNN của
P=2x4+x3(2y-1)+y3(2x-1)+2y4
Các số thực x, y thỏa mãn:
(
2
x
+
3
y
+
1
)
+
(
-
x
+
2
y
)
i
(
3
x
-
2
y
+
2
)
+
(
4...
Đọc tiếp
Các số thực x, y thỏa mãn: ( 2 x + 3 y + 1 ) + ( - x + 2 y ) i = ( 3 x - 2 y + 2 ) + ( 4 x - y - 3 ) i là
A. x ; y = - 9 11 ; - 4 11
B. x ; y = 9 11 ; 4 11
C. x ; y = 9 11 ; - 4 11
D. x ; y = - 9 11 ; 4 11
1. Tìm GTNN Cho x,y là các số thực thỏa mãn x+y=của P=2x3+x3(2y-1)+y3(2x-1)+2y4
Sửa: \(P=2x^4+x^3\left(2y-1\right)+y^3\left(2x-1\right)+2y^4\); x+y=1
Ta có \(P=2x^4+x^3\left(2y-1\right)+y^3\left(2x-1\right)+2y^4=2x^4+2x^3y-x^3+2xy^3-y^3+2y^4\)
\(=x^3\left(2x+2y\right)+y^3\left(2x+2y\right)-\left(x^3+y^3\right)=\left(2x+2y\right)\left(x^3+y^3\right)-\left(x^3+y^3\right)\)
\(=\left(2x+2y-1\right)\left(x^3+y^3\right)=x^3+y^3\)
Do \(x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)=x^2-xy+y^2=\frac{1}{2}\left(x^2+y^2\right)\left(\frac{x}{\sqrt{2}}-\frac{y}{\sqrt{2}}\right)^2\)
\(\Rightarrow P\ge\frac{1}{2}\left(x^2+y^2\right)\)
Mà \(x+y=1\Rightarrow x^2+y^2+2xy=1\Rightarrow2\left(x^2+y^2\right)-\left(x-y\right)^2=1\)
\(\Rightarrow2\left(x^2+y^2\right)\ge1\Rightarrow\left(x^2+y^2\right)\ge\frac{1}{2}\Rightarrow P\ge\frac{1}{4}\)
Dấu "=" xảy ra khi \(x=y=\frac{1}{2}\)
CHO 2 SỐ THỰC X;Y THỎA MÃN X^2 +Y^2 =1.GIÁ TRỊ BIỂU THỨC A=X^4+2X^2Y^2+X^2+Y^4+Y^2 LÀ:
cho các số thực x,y thõa mãn x^4 + y^4 + x^2 - 3 - 2y^2x(1-x^2) tìm gtln của x^2 + y^2
Đề thiếu. Bạn viết lại đề cẩn thận, rõ ràng để mọi người hỗ trợ tốt hơn bạn nhé.
Đúng 0
Bình luận (0)
cho 2 số thực `x,y` thỏa mãn `x>0,y>2,x`\(\ne\)`2y`. CMR: \(\left(\dfrac{x-y}{2y-x}-\dfrac{x^2+y^2+y-2}{x^2-xy-2y^2}\right)\left(2x^2+y+2\right):\dfrac{x^4+4x^2y^2+y^4-4}{x^2+y+xy+x}=\dfrac{x+1}{2y-x}\)
Đề bài sai, đề đúng thì phân thức đằng sau dấu chia phải là:
\(\dfrac{4x^4+4x^2y+y^2-4}{x^2+y+xy+x}\)
Đúng 0
Bình luận (0)