bài 8 sgk 7 hình trang 109
H24
Những câu hỏi liên quan
Các bạn ơi làm giúp mình bài 6 ( Sgk / hình 56 / trang 109 ) chương II : Tam Gíac
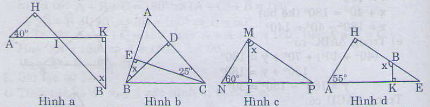
Hình a)
Ta có = 900,
+
= 900
mà =
( đối đỉnh)
Suy ra =
Vậy = 400
Hình b) Ta có +
= 900,
+
=900,
Suy ra =
Vậy = 250,
Hình c) Ta có: +
= 900,
+
= 900,
Suy ra =
Vậy = 600
Hình d) ta có
= 900 -
= 900 - 550 = 350
= 900 +
(Góc ngoài tam giác BKE)
= 900 + 350 = 1250
Đúng 0
Bình luận (1)
Cần gấp !!!!!!!!!!!!!!
Bài 9 sgk toán 7 tập 1 trang 109.
vietjack.com
Tam giác ABC vuông tại A nên ˆABC+ˆACB=90o (1)
Tam giác DOC vuông tại D nên ˆCOD+ˆOCD=900 (2)
Ta lại có ˆACB=ˆOCD (đối đỉnh) (3)
Từ (1), (2), (3) suy ra ˆCOD=ˆABCC Vậy ˆMOP=320
Tam giác ABC vuông tại A nên góc ABC + góc ACB = 90o (1)
Tam giác DOC vuông tại góc D nên góc COD + góc OCD=90o (2)
Ta lại có góc ACB = góc OCD (đối đỉnh) (3)
Từ (1), (2), (3) suy ra góc COD = góc ABC . Vậy góc MOP = 32o
Xem thêm câu trả lời
toán hình bài 6 sgk lớp 7 trang 109
Đề đây à bn?
Bài 6. Tìm các số đo xx ở các hình sau:
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Câu 1 trang 109 SGK văn 7 tập 2 KNTT (mẫu)
Xem chi tiết
Em nhập ndung câu hỏi vào em hi
Đúng 0
Bình luận (0)
bài 17 trang 109 (sgk) lớp 6 tập 1
bn bị điên à câu hỏi thì chẳng có trả lời vào đâu
Đúng 0
Bình luận (0)
mọi người ơi giúp mình trả lời câu hỏi ôn tập lớp 7 chương 3 hình học kì 2( tư bài 1 đến bài 8) với! trang 86 (sgk) lớp 7 hình học nha
ghi rõ bài ra người ta giải cho
bạn phải ghi rõ câu hỏi ra
các bạn giúp mk giải bài tập 18 bài đường thẳng đi qua hai điểm giùm minh nha.trong sgk trang 109
Giả sử 
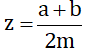
Xem thêm câu trả lời
Giả sử 
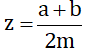
Cái bài này mình đã từng đăng để hỏi mấy bạn kia.
Nhưng đề câu này thiểu bạn ơi.
Phải có x=a/m ; y=b/m
À thôi, mk viết đầy đủ đề thử nhé !
Giả sử:x=a/m;y=b/m (a,b,m thuộc Z.m > 0) và x < y.
Hãy chứng minh (chứng tỏ) rằng nếu chọn z=a+b/2m thì ta có x < y < z.
Trong sách lớp 7 đề y như z đó !
Mk ghi cách làm luôn nha !
Giả sử x=a/m,y=b/m (a,b,m thuộc Z,m > 0 )
Vì x < y nên ta suy ra a < b.
ta có: x=a/m, y=b/m <=> x=2a/am. y=2b/2m
mà a < b nên a+a < a+b <=> 2a < a+b
Do 2a < a+b thì x < y ( 1 )
Ta lại có: a < b nên a+b < b+b <=> a+b < 2b
Mà a+b < 2b <=> x < z ( 2 )
Từ ( 1 ) và ( 2 ) suy ra x < y < z (ĐPCM)
Đúng 0
Bình luận (0)



