Vẽ hình và giả thiết , kl lun vs ạ
HT
Những câu hỏi liên quan

giả thết kết luận và vẽ hình lun ạ
Cần gấp ạ
Bài 4:
a: \(BC=\sqrt{8^2+6^2}=10\left(cm\right)\)
b: Xét ΔEDB có
EA là đường cao
EA là đường trung tuyến
Do đó:ΔEDB cân tại E
Xét ΔCDB có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCDB cân tại C
Xét ΔCDE và ΔCBE có
CD=CB
ED=EB
CE chung
Do đó: ΔCDE=ΔCBE
c: Xét ΔCDB có
CA là đường trung tuyến
CE=2/3CA
Do đó: E là trọng tâm của ΔCDB
Suy ra: DE đi qua trung điểm của BC
Đúng 4
Bình luận (1)
Bài 2 ạ. Nhờ mn vẽ hình và giả thiết, kết luận với ạ

vẽ hình, giả thiết kết luận và giải luôn ạ
Câu 3:
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
Suy ra:HB=HC
b: Ta có: ΔAHB=ΔAHC
nên \(\widehat{BAH}=\widehat{CAH}\)
c: Ta có:ΔABC cân tại A
mà AH là đường cao
nên AH là tia phân giác của góc BAC
Đúng 0
Bình luận (2)
Xem thêm câu trả lời

vẽ hình, giả thiết, kết luaanvaf giải bài 3 và 4 nx ạ
Câu 3:
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
DO đó: ΔABH=ΔACH
Suy ra: BH=CH
b: Ta có: ΔABH=ΔACH
nên \(\widehat{BAH}=\widehat{CAH}\)
c: Ta có: ΔABC cân tại A
mà AH là đường phân giác
nên AH là tia phân giác của góc BAC
Đúng 2
Bình luận (1)
Xem thêm câu trả lời

vẽ hình, giả thiết kết luận và giải chomik bài 3 vsf 4 với ạ
Mọi người giúp e bài 4 vs ạ vẽ hình và viết gt, kl cảm ơn mọi người

Giup mik câu 4 vs ạ giup mik vẽ hình lun vs
Dựa vào giả thiết và kết luận dưới đây, hãy vẽ hình và giải
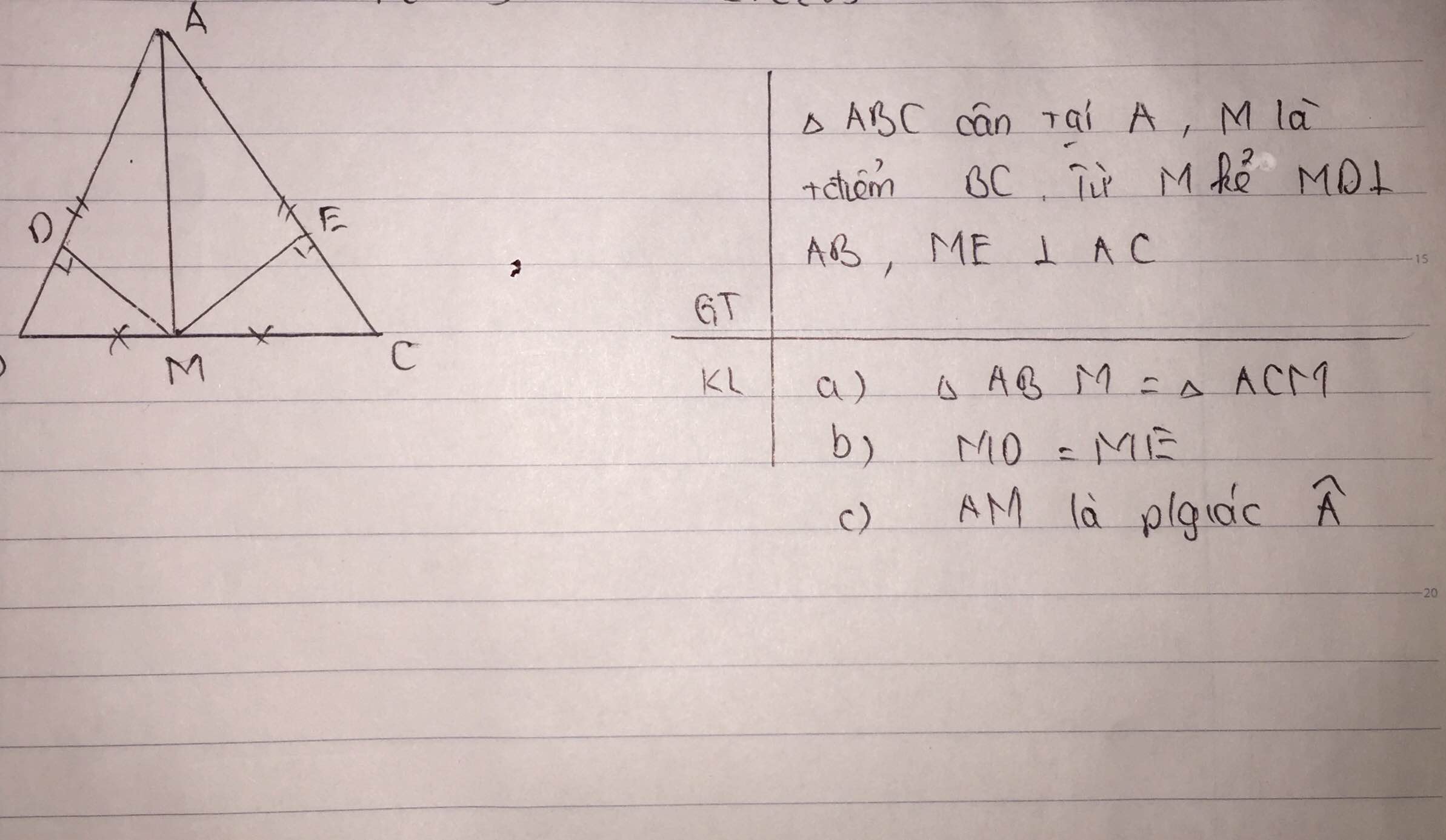
GT: Δ ABC vuông tại A
AH⊥ BC
MC=CA (M ∈ BC)
AN=AH (N ∈ BA)
KL: a, ∠CAM=∠CMA
b, ∠CMA và ∠MAN phụ nhau
c, AN là tia phân giác ∠BAH
d, MN⊥AB
a) Xét ΔCAM có CA=CM(gt)
nên ΔCAM cân tại C(Định nghĩa tam giác cân)
\(\Leftrightarrow\widehat{CAM}=\widehat{CMA}\)(hai góc ở đáy)
b) Ta có: \(\widehat{MAB}+\widehat{MAC}=\widehat{BAC}\)(tia AM nằm giữa hai tia AB,AC)
\(\Leftrightarrow\widehat{MAN}+\widehat{CAM}=90^0\)
mà \(\widehat{CAM}=\widehat{CMA}\)(cmt)
nên \(\widehat{CMA}+\widehat{MAN}=90^0\)
hay \(\widehat{CMA};\widehat{MAN}\) là hai góc phụ nhau(đpcm)
Đúng 2
Bình luận (0)
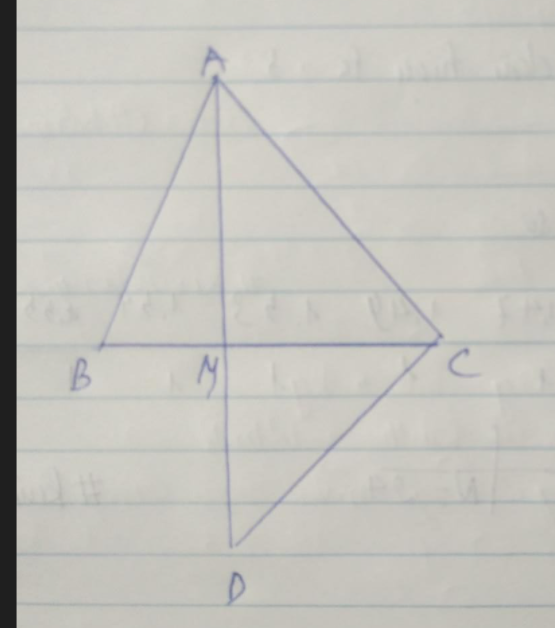
△ ABC có đường trung tuyến AM đồng thời là đường phân giác. Trên tia AM lấy điểm D sao cho MD=MA. CMR:
a) AB=CD
b) △ACD cân tại A
c) △ABC cân tại A
(vẽ hình và ghi giả thiết kl)
a: Xét ΔAMB và ΔDMC có
MA=MD
AMB=DMC
MB=MC
Do đó: ΔAMB=ΔDMC
Suy ra: AB=CD
c: Xét ΔABC có
AM là đường trung tuyến ứng với cạnh BC
AM là đường phân giác ứng với cạnh BC
Do đó: ΔABC cân tại A
Đúng 3
Bình luận (2)