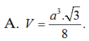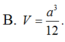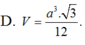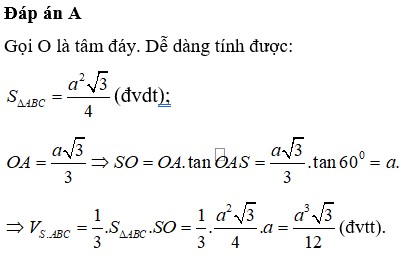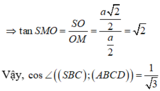Cho hình chóp đều SABC tất cả các cạnh bằng a.Xác định góc giữa cạnh bên và mặt phẳng đáy
KA
Những câu hỏi liên quan
Cho hình chóp đều SABC, cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng
60
°
. Tính thể tích của khối chóp SABC A.
a
3
3
12
B.
a
3
12
C.
a
3
3
4...
Đọc tiếp
Cho hình chóp đều SABC, cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60 ° . Tính thể tích của khối chóp SABC
A. a 3 3 12
B. a 3 12
C. a 3 3 4
D. a 3 3 36
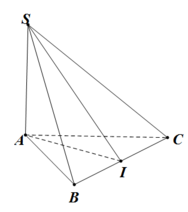
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng
60
°
. Thể tích của khối chóp SABC bằng A.
a
3
3
8
B.
a
3
12
C.
a
3...
Đọc tiếp
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60 ° . Thể tích của khối chóp SABC bằng
A. a 3 3 8
B. a 3 12
C. a 3 3 4
D. a 3 3 12
Cho hình chóp SABC có đáy là tam giác đều cạnh
α
, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 600. Thể tích của khối chóp SABC bằng
Đọc tiếp
Cho hình chóp SABC có đáy là tam giác đều cạnh α , SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 600. Thể tích của khối chóp SABC bằng
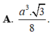
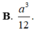
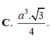
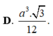
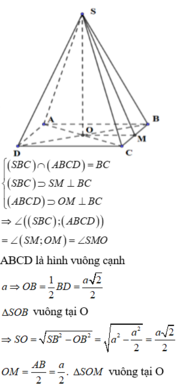
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a . Tính góc giữa cạnh bên và mặt đáy .
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Tan của góc giữa mặt bên và mặt đáy bằng:
A. 2
B. 2 2
C. 3 2
D. 3
Đáp án A.
- Phương pháp:
+) Xác định góc giữa mặt bên và đáy là góc giữa hai đường thẳng lần lượt thuộc 2 mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng đó.
+) Tính tan của góc xác định được.
Cách giải:
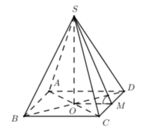
- Gọi O = AC ∩ BD. Do S.ABCD là chóp đều ⇒ SO ⊥ (ABCD).
- Gọi M là trung điểm của CD ta có: OM là đường trung bình của tam giác BCD ⇒ OM // BC ⇒ OM ⊥ CD.
- Ta có:

- Áp dụng định lý Pytago trong tam giác vuông SOM ta có:
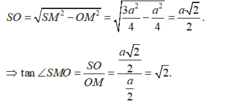
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Côsin góc giữa mặt bên và mặt đáy là A.
1
3
B.
1
3
C.
1
2
D.
1
2
Đọc tiếp
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Côsin góc giữa mặt bên và mặt đáy là
A. 1 3
B. 1 3
C. 1 2
D. 1 2
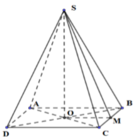
Gọi M là trung điểm của BC. Ta có: O M ⊥ B C S O ⊥ B C ⇒ B C ( S O M )
⇒ B C ⊥ S M
Ta có:
S B C ⊥ A B C D = B C S S B C ⊃ S M ⊥ B C ( A B C D ) ⊃ O M ⊥ B C ⇒ ∠ S B C , A B C D = ∠ S M ; O M = ∠ S M O
ABCD là hình vuông cạnh a ⇒ O B = 1 2 B D = a 2 2
∆ S O B vuông tại O ⇒ S O = S B 2 - O B 2
= a 2 - a 2 2 = a 2 2
O M = A B 2 = a 2 . ∆ S O M vuông tại O
⇒ tan S M O = S O O M = a 2 2 a 2 = 2
Vậy, cos ∠ S B C , A B C D = 1 3
Chọn đáp án A.
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Côsin góc giữa mặt bên và mặt đáy là: A.
1
3
B.
1
3
C.
1
2
D.
1
2
Đọc tiếp
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Côsin góc giữa mặt bên và mặt đáy là:
A. 1 3
B. 1 3
C. 1 2
D. 1 2
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Côsin góc giữa mặt bên và mặt đáy là:
A. 1 3
B. 1 3
C. 1 2
D. 1 2
Phương pháp:
Xác định góc giữa hai mặt phẳng ![]()
- Tìm giao tuyến
∆
của ![]()
- Xác định 1 mặt phẳng ![]()
- Tìm các giao tuyến ![]()
- Góc giữa hai mặt phẳng ![]()
![]()
Cách giải:
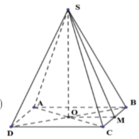
Gọi M là trung điểm của BC. Ta có:
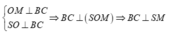
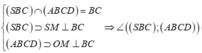
![]()
ABCD là hình vuông cạnh a
![]()
∆ SOB vuông tại O
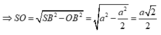
![]()
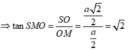
![]()
Chọn: A
Đúng 0
Bình luận (0)
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng
60
0
. Tính thể tích V của khối chóp SABC.
Đọc tiếp
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60 0 . Tính thể tích V của khối chóp SABC.